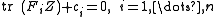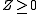Conic optimization
Encyclopedia
Conic optimization is a subfield of convex optimization that studies a class of structured convex optimization problems called conic optimization problems. A conic optimization problem consists of minimizing a convex function
over the intersection of an affine subspace and a convex cone
.
The class of conic optimization problems is a subclass of convex optimization problems and it includes some of the most well known classes of convex optimization problems, namely linear
and semidefinite programming
.
vector space
X, a convex
, real-valued function
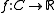
defined on a convex cone
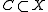 , and an affine subspace
, and an affine subspace  defined by a set of affine
defined by a set of affine
constraints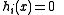 , a conic optimization problem is to find the point
, a conic optimization problem is to find the point  in
in 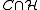 for which the number
for which the number 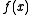 is smallest. Examples of
is smallest. Examples of  include the positive semidefinite
include the positive semidefinite
matrices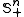 , the positive orthant
, the positive orthant 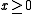 for
for 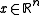 , and the second-order cone
, and the second-order cone  . Often
. Often 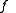 is a linear function, in which case the conic optimization problem reduces to a semidefinite program
is a linear function, in which case the conic optimization problem reduces to a semidefinite program
, a linear program, and a second order cone program, respectively.
is
where denotes the dual cone of
denotes the dual cone of 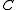 .
.
minimize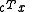 subject to
subject to
is given by
maximize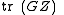 subject to
subject to
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
over the intersection of an affine subspace and a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
.
The class of conic optimization problems is a subclass of convex optimization problems and it includes some of the most well known classes of convex optimization problems, namely linear
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
and semidefinite programming
Semidefinite programming
Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
.
Definition
Given a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
X, a convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, real-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
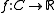
defined on a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
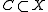 , and an affine subspace
, and an affine subspace  defined by a set of affine
defined by a set of affineAffine
Affine may refer to:*Affine cipher, a special case of the more general substitution cipher*Affine combination, a certain kind of constrained linear combination*Affine connection, a connection on the tangent bundle of a differentiable manifold...
constraints
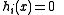 , a conic optimization problem is to find the point
, a conic optimization problem is to find the point  in
in 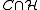 for which the number
for which the number 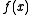 is smallest. Examples of
is smallest. Examples of  include the positive semidefinite
include the positive semidefinitePositive semidefinite
In mathematics, positive semidefinite may refer to:* positive-semidefinite matrix* positive-semidefinite function...
matrices
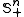 , the positive orthant
, the positive orthant 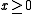 for
for 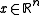 , and the second-order cone
, and the second-order cone  . Often
. Often 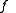 is a linear function, in which case the conic optimization problem reduces to a semidefinite program
is a linear function, in which case the conic optimization problem reduces to a semidefinite programSemidefinite programming
Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
, a linear program, and a second order cone program, respectively.
Duality
Certain special cases of conic optimization problems have notable closed-form expressions of their dual problems.Conic LP
The dual of the conic linear program- minimize
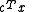
- subject to
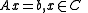
is
- maximize
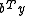
- subject to
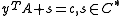
where
 denotes the dual cone of
denotes the dual cone of 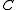 .
.Semidefinite Program
The dual of a semidefinite program in inequality form,minimize
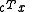 subject to
subject tois given by
maximize
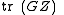 subject to
subject toExternal links
- MOSEK Software capable of solving conic optimization problems.