
Configuration entropy
Encyclopedia
In statistical mechanics
, configuration entropy is the portion of a system's entropy
that is related to the position of its constituent particles rather than to their velocity
or momentum
. It is physically related to the number of ways of arranging all the particle
s of the system while maintaining some overall set of specified system properties, such as energy
. The configurational entropy is also known as microscopic entropy or conformational entropy
in the study of macromolecules. In general, configurational entropy is the foundation of statistical thermodynamics.
It can be shown that the variation of configuration entropy of thermodynamic systems (e.g., ideal gas, and other systems with a vast number of internal degrees of freedom) in thermodynamic processes is equivalent to the variation of the macroscopic entropy defined as dS = δQ/T, where δQ is the heat
exchanged between the system and the surrounding media, and T is temperature. Therefore configuration entropy is the same as macroscopic entropy.
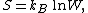
where kB is the Boltzmann constant and W is the number of possible configurations. In a more general formulation, if a system can be in states n with probabilities Pn, the configurational entropy of the system is given by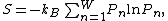
which in the perfect disorder limit (all Pn = 1/W) leads to Boltzmann's formula, while in the opposite limit (one configuration with probability 1), the entropy vanishes. This formulation is analogous to that of Shannon's information entropy.
The mathematical field of combinatorics
, and in particular the mathematics
of combination
s and permutation
s is highly important in the calculation of configurational entropy. In particular, this field of mathematics offers formalized approaches for calculating the number of ways of choosing or arranging discrete objects; in this case, atom
s or molecule
s. However, it is important to note that the positions of molecules are not strictly speaking discrete above the quantum level. Thus a variety of approximations may be used in discretizing a system to allow for a purely combinatorial approach. Alternatively, integral methods may be used in some cases to work directly with continuous position functions.
A second approach used (most often in computer simulations, but also analytically) to determine the configurational entropy is the Widom insertion method
.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, configuration entropy is the portion of a system's entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
that is related to the position of its constituent particles rather than to their velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
or momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. It is physically related to the number of ways of arranging all the particle
Particle
A particle is, generally, a small localized object to which can be ascribed physical properties. It may also refer to:In chemistry:* Colloidal particle, part of a one-phase system of two or more components where the particles aren't individually visible.In physics:* Subatomic particle, which may be...
s of the system while maintaining some overall set of specified system properties, such as energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
. The configurational entropy is also known as microscopic entropy or conformational entropy
Conformational entropy
Conformational entropy is the entropy associated with the physical arrangement of a polymer chain that assumes a compact or globular state in solution. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but can also be used for polysaccharides and other...
in the study of macromolecules. In general, configurational entropy is the foundation of statistical thermodynamics.
It can be shown that the variation of configuration entropy of thermodynamic systems (e.g., ideal gas, and other systems with a vast number of internal degrees of freedom) in thermodynamic processes is equivalent to the variation of the macroscopic entropy defined as dS = δQ/T, where δQ is the heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
exchanged between the system and the surrounding media, and T is temperature. Therefore configuration entropy is the same as macroscopic entropy.
Calculation
The configurational entropy is related to the number of possible configurations by Boltzmann's entropy formulaBoltzmann's entropy formula
In statistical thermodynamics, Boltzmann's equation is a probability equation relating the entropy S of an ideal gas to the quantity W, which is the number of microstates corresponding to a given macrostate:...
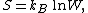
where kB is the Boltzmann constant and W is the number of possible configurations. In a more general formulation, if a system can be in states n with probabilities Pn, the configurational entropy of the system is given by
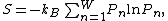
which in the perfect disorder limit (all Pn = 1/W) leads to Boltzmann's formula, while in the opposite limit (one configuration with probability 1), the entropy vanishes. This formulation is analogous to that of Shannon's information entropy.
The mathematical field of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, and in particular the mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s and permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s is highly important in the calculation of configurational entropy. In particular, this field of mathematics offers formalized approaches for calculating the number of ways of choosing or arranging discrete objects; in this case, atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s or molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s. However, it is important to note that the positions of molecules are not strictly speaking discrete above the quantum level. Thus a variety of approximations may be used in discretizing a system to allow for a purely combinatorial approach. Alternatively, integral methods may be used in some cases to work directly with continuous position functions.
A second approach used (most often in computer simulations, but also analytically) to determine the configurational entropy is the Widom insertion method
Widom insertion method
The Widom Insertion Method is a statistical thermodynamic approach to the calculation of material and mixture properties. It is named for Benjamin Widom, who derived it in 1963. In general, there are two theoretical approaches to determining the statistical mechanical properties of materials...
.
See also
- Conformational entropyConformational entropyConformational entropy is the entropy associated with the physical arrangement of a polymer chain that assumes a compact or globular state in solution. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but can also be used for polysaccharides and other...
- CombinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
- Entropic forceEntropic forceIn physics, an entropic force acting in a system is a phenomenological force resulting from the entire system's statistical tendency to increase its entropy, rather than from a particular underlying microscopic force.-Polymers:...
- NanomechanicsNanomechanicsNanomechanics is a branch of nanoscience studying fundamental mechanical properties of physical systems at the nanometer scale. Nanomechanics has emerged on the crossroads of classical mechanics, solid-state physics, statistical mechanics, materials science, and quantum chemistry...
- Entropy of mixingEntropy of mixingIn thermodynamics the entropy of mixing is the increase in the total entropy of a compound system, when different and chemically non-reacting chemical substances or material components are mixed by removing partition between the system's initially separate volumes...

