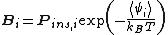Widom insertion method
Encyclopedia
The Widom Insertion Method is a statistical thermodynamic approach to the calculation of material and mixture properties. It is named for Benjamin Widom, who derived it in 1963. In general, there are two theoretical approaches to determining the statistical mechanical properties of materials. The first is the direct calculation of the overall Partition Function
of the system, which directly yields the system free energy. The second approach, known as the Widom Insertion method, instead derives from calculations centering around one molecule. The Widom Insertion method directly yields the chemical potential of one component rather than the system free energy. This approach is most widely applied in molecular computer simulations but has also been applied in the development of analytical statical mechanical models.
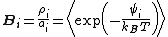
where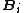 is called the 'insertion parameter',
is called the 'insertion parameter',  is the number density of species
is the number density of species 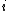 ,
,  is the activity
is the activity
of species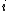 ,
, 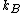 is the Boltzmann constant, and
is the Boltzmann constant, and 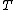 is temperature, and
is temperature, and 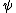 is the interaction energy of an inserted particle with all other particles in the system. The average is over all possible insertions. This can be understood conceptually as fixing the location of all molecules in the system and then inserting a particle of species
is the interaction energy of an inserted particle with all other particles in the system. The average is over all possible insertions. This can be understood conceptually as fixing the location of all molecules in the system and then inserting a particle of species 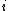 at all locations through the system, averaging over a Boltzmann factor
at all locations through the system, averaging over a Boltzmann factor
in its interaction energy over all of those locations.
by
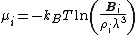
of a mixture is related to the insertion parameter via
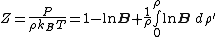
where is the compressibility factor
is the compressibility factor
,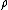 is the overall number density of the mixture, and
is the overall number density of the mixture, and  is a mole-fraction weighted average over all mixture components:
is a mole-fraction weighted average over all mixture components:
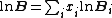
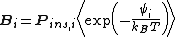
where is the probability that the randomly inserted molecule of species
is the probability that the randomly inserted molecule of species 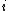 will experience and attractive or zero net interaction; in other words, it is the probability that the inserted molecule does not 'overlap' with any other molecules.
will experience and attractive or zero net interaction; in other words, it is the probability that the inserted molecule does not 'overlap' with any other molecules.
, which essentially ignores fluctuations and treats all quantities by their average value. Within this framework the insertion factor is given as
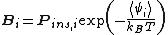
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of the system, which directly yields the system free energy. The second approach, known as the Widom Insertion method, instead derives from calculations centering around one molecule. The Widom Insertion method directly yields the chemical potential of one component rather than the system free energy. This approach is most widely applied in molecular computer simulations but has also been applied in the development of analytical statical mechanical models.
Overview
As originally formulated by Benjamin Widom in 1963, the approach can be summarized by the equation: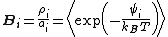
where
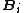 is called the 'insertion parameter',
is called the 'insertion parameter', 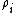 is the number density of species
is the number density of species 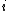 ,
,  is the activity
is the activityActivity (chemistry)
In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
of species
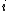 ,
, 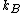 is the Boltzmann constant, and
is the Boltzmann constant, and 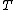 is temperature, and
is temperature, and 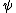 is the interaction energy of an inserted particle with all other particles in the system. The average is over all possible insertions. This can be understood conceptually as fixing the location of all molecules in the system and then inserting a particle of species
is the interaction energy of an inserted particle with all other particles in the system. The average is over all possible insertions. This can be understood conceptually as fixing the location of all molecules in the system and then inserting a particle of species 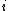 at all locations through the system, averaging over a Boltzmann factor
at all locations through the system, averaging over a Boltzmann factorBoltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
in its interaction energy over all of those locations.
Chemical Potential
From the above equation and from the definition of activity, the insertion parameter may be related to the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
by
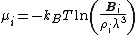
Equation of State
The Pressure-Temperature-Density relation, or equation of stateEquation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
of a mixture is related to the insertion parameter via
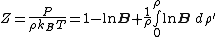
where
 is the compressibility factor
is the compressibility factorCompressibility factor
The compressibility factor , also known as the compression factor, is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior. In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the...
,
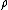 is the overall number density of the mixture, and
is the overall number density of the mixture, and  is a mole-fraction weighted average over all mixture components:
is a mole-fraction weighted average over all mixture components: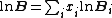
Hard Core Model
In the case of a 'hard core' repulsive model in which each molecule or atom consists of a hard core with an infinite repulsive potential, insertions in which two molecules occupy the same space will not contribute to the average. In this case the insertion parameter becomes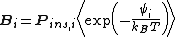
where
 is the probability that the randomly inserted molecule of species
is the probability that the randomly inserted molecule of species 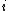 will experience and attractive or zero net interaction; in other words, it is the probability that the inserted molecule does not 'overlap' with any other molecules.
will experience and attractive or zero net interaction; in other words, it is the probability that the inserted molecule does not 'overlap' with any other molecules.Mean Field Approximation
The above is simplified further via the application of the mean field approximationMean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
, which essentially ignores fluctuations and treats all quantities by their average value. Within this framework the insertion factor is given as