Confidence region
Encyclopedia
In statistics
, a confidence region is a multi-dimensional generalization of a confidence interval
. It is a set of points in an n-dimensional space, often represented as an ellipsoid around a point which is an estimated solution to a problem, although other shapes can occur.
The confidence region is calculated in such a way that if a set of measurements were repeated many times and a confidence region calculated in the same way on each set of measurements, then a certain percentage of the time, on average, (e.g. 95%) the confidence region would include the point representing the "true" values of the set of variables being estimated. However, it does not mean, when one confidence region has been calculated, that there is a 95% probability that the "true" values lie inside the region, since we do not assume any particular probability distribution of the "true" values and we may or may not have other information about where they are likely to lie.
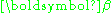to the following overdetermined problem: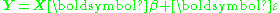
where Y is an n-dimensional column vector containing observed values, X is an n-by-p matrix which can represent a physical model and which is assumed to be known exactly,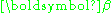
is a column vector containing the p parameters which are to be estimated, and 
is an n-dimensional column vector of errors which are assumed to be independently distributed
with normal distributions with zero mean and each having the same unknown variance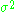
.
A joint 100(1 -
) % confidence region for the elements of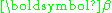 
is represented by the set of values of the vector b which satisfy the following inequality:
where the variable b represents any point in the confidence region, p is the number of parameters, i.e. number of elements of the vector
and s2 is an unbiased estimate of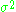 
equal to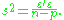
Further, F is the quantile function
of the F-distribution, with p and
degrees of freedom
,
is the statistical significance
level, and the symbol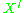
means the transpose
of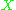
.
The above inequality defines an ellipsoidal region in the p-dimensional Cartesian parameter space Rp. The centre of the ellipsoid is at the solution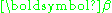
. According to Press et al., it's easier to plot the ellipsoid after doing singular value decomposition
. The lengths of the axes of the ellipsoid are proportional to the reciprocals of the values on the diagonals of the diagonal matrix, and the directions of these axes are given by the rows of the 3rd matrix of the decomposition.
have known nonzero covariance
(in other words, the errors in the observations are not independently distributed), and/or the standard deviations of the errors are not all equal. Suppose the covariance matrix of
is 
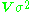, where V is an n-by-n nonsingular matrix which was equal to 
in the more specific case handled in the previous section, (where I is the identity matrix
,) but here is allowed to have nonzero off-diagonal elements representing the covariance of pairs of individual observations, as well as not necessarily having all the diagonal elements equal.
It is possible to find a nonsingular symmetric matrix P such that
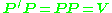
In effect, P is a square root of the covariance matrix V.
The least-squares problem
can then be transformed by left-multiplying each term by the inverse of P, forming the new problem formulation
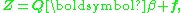
where
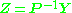
A joint confidence region for the parameters, i.e. for the elements of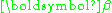
, is then bounded by the ellipsoid given by:
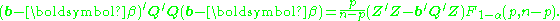
Here F represents the percentage point of the F distribution and the quantities p and n-p are the degrees of freedom
which are the parameters of this distribution.
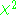(chi-squared
) values.
One approach is to use a linear approximation to the nonlinear model, which may be a close approximation in the vicinity of the solution, and then apply the analysis for a linear problem to find an approximate confidence region. This may be a reasonable approach if the confidence region is not very large and the second derivatives of the model are also not very large.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a confidence region is a multi-dimensional generalization of a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
. It is a set of points in an n-dimensional space, often represented as an ellipsoid around a point which is an estimated solution to a problem, although other shapes can occur.
The confidence region is calculated in such a way that if a set of measurements were repeated many times and a confidence region calculated in the same way on each set of measurements, then a certain percentage of the time, on average, (e.g. 95%) the confidence region would include the point representing the "true" values of the set of variables being estimated. However, it does not mean, when one confidence region has been calculated, that there is a 95% probability that the "true" values lie inside the region, since we do not assume any particular probability distribution of the "true" values and we may or may not have other information about where they are likely to lie.
The case of independent, identically normally-distributed errors
Suppose we have found a solution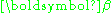 to the following overdetermined problem: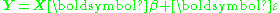where Y is an n-dimensional column vector containing observed values, X is an n-by-p matrix which can represent a physical model and which is assumed to be known exactly,
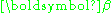is a column vector containing the p parameters which are to be estimated, and is an n-dimensional column vector of errors which are assumed to be independently distributedStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
with normal distributions with zero mean and each having the same unknown variance
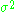.A joint 100(1 -
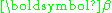) % confidence region for the elements of is represented by the set of values of the vector b which satisfy the following inequality:where the variable b represents any point in the confidence region, p is the number of parameters, i.e. number of elements of the vector
and s2 is an unbiased estimate of 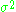equal to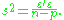Further, F is the quantile function
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
of the F-distribution, with p and
degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
,
is the statistical significanceStatistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
level, and the symbol
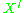means the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of
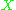.The above inequality defines an ellipsoidal region in the p-dimensional Cartesian parameter space Rp. The centre of the ellipsoid is at the solution
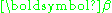. According to Press et al., it's easier to plot the ellipsoid after doing singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
. The lengths of the axes of the ellipsoid are proportional to the reciprocals of the values on the diagonals of the diagonal matrix, and the directions of these axes are given by the rows of the 3rd matrix of the decomposition.
Weighted and generalised least squares
Now let us consider the more general case where some distinct elements of have known nonzero covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
(in other words, the errors in the observations are not independently distributed), and/or the standard deviations of the errors are not all equal. Suppose the covariance matrix of
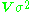is , where V is an n-by-n nonsingular matrix which was equal to in the more specific case handled in the previous section, (where I is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
,) but here is allowed to have nonzero off-diagonal elements representing the covariance of pairs of individual observations, as well as not necessarily having all the diagonal elements equal.
It is possible to find a nonsingular symmetric matrix P such that
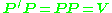
In effect, P is a square root of the covariance matrix V.
The least-squares problem
can then be transformed by left-multiplying each term by the inverse of P, forming the new problem formulation
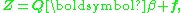
where
-
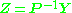
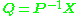and
A joint confidence region for the parameters, i.e. for the elements of
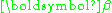, is then bounded by the ellipsoid given by: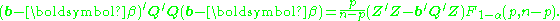Here F represents the percentage point of the F distribution and the quantities p and n-p are the degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
which are the parameters of this distribution.
Nonlinear problems
Confidence regions can be defined for any probability distribution. The experimenter can choose the significance level and the shape of the region, and then the size of the region is determined by the probability distribution. A natural choice is to use as a boundary a set of points with constant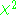 (chi-squaredChi-squared
In statistics, the term chi-squared has different uses:*chi-squared distribution, a continuous probability distribution;*chi-squared statistic, a statistic used in some statistical tests;...
) values.
One approach is to use a linear approximation to the nonlinear model, which may be a close approximation in the vicinity of the solution, and then apply the analysis for a linear problem to find an approximate confidence region. This may be a reasonable approach if the confidence region is not very large and the second derivatives of the model are also not very large.
External links
- Error ellipses, University of Melbourne, Australia