
Concatenated error correction codes
Encyclopedia
In coding theory
, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity
.
Concatenated codes became widely used in space communications in the 1970s.
Shannon's channel coding theorem shows that over many common channels there exist channel coding schemes that are able to transmit data reliably at all rates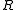 less than a certain threshold
less than a certain threshold  , called the channel capacity
, called the channel capacity
of the given channel. In fact, the probability of decoding error can be made to decrease exponentially as the block length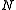 of the coding scheme goes to infinity. However, the complexity of a naive optimum decoding scheme that simply computes the likelihood of every possible transmitted codeword increases exponentially with
of the coding scheme goes to infinity. However, the complexity of a naive optimum decoding scheme that simply computes the likelihood of every possible transmitted codeword increases exponentially with 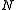 , so such an optimum decoder rapidly becomes infeasible.
, so such an optimum decoder rapidly becomes infeasible.
In his doctoral thesis, Dave Forney showed that concatenated codes could be used to achieve exponentially decreasing error probabilities at all data rates less than capacity, with decoding complexity that increases only polynomially with the code block length.
of length n, dimension
k, minimum Hamming distance
d, and rate
r = n/k, over an alphabet A:
Let Cout be a [N, K, D] code over an alphabet B with |B| = |A|k symbols: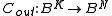
The inner code Cin takes one of |A|k = |B| possible inputs, encodes into an n-tuple over A, transmits, and decodes into one of |B| possible outputs. We regard this as a (super) channel which can transmit one symbol from the alphabet B. We use this channel N times to transmit each of the N symbols in a codeword of Cout. The concatenation of Cout (as outer code) with Cin (as inner code), denoted Cout∘Cin, is thus a code of length Nn over the alphabet A: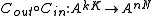
It maps each input message m = (m1, m2, ..., mK) to a codeword (Cin(m' 1), Cin(m' 2), ..., Cin(m' N)),
where (m' 1, m' 2, ..., m' N) = Cout(m1, m2, ..., mK).
The key insight in this approach is that if Cin is decoded using a maximum-likelihood approach (thus showing an exponentially decreasing error probability with increasing length), and Cout is a code with length N = 2nr that can be decoded in polynomial time of N, then the concatenated code can be decoded in polynomial time of its combined length n2nr = O(N⋅log(N)) and shows an exponentially decreasing error probability, even if Cin has exponential decoding complexity. This is discussed in more detail in section Decoding concatenated codes.
In a generalization of above concatenation, there are N possible inner codes Cin,i and the i-th symbol in a codeword of Cout is transmitted across the inner channel using the i-th inner code. The Justesen codes are examples of generalized concatenated codes, where the outer code is a Reed-Solomon code.
' ] code with D' ≥ dD.
Proof:
Consider two different messages m1 ≠ m2 ∈ BK. Let Δ denote the distance between two codewords. Then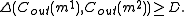
Thus, there are at least D positions in which the sequence of N symbols of the codewords Cout(m1) and Cout(m2) differ. For these positions, denoted i, we have
Consequently, there are at least d⋅D positions in the sequence of n⋅N symbols taken from the alphabet A in which the two codewords differ, and hence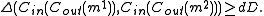
2. If Cout and Cin are linear block codes, then Cout∘Cin is also a linear block code.
This property can be easily shown based on the idea of defining a generator matrix
for the concatenated code in terms of the generator matrices of Cout and Cin.
In detail, let the input to the decoder be the vector y = (y1, ..., yN) ∈ (An)N. Then the decoding algorithm is a two-step process:
Now, the time complexity of the first step is O(N⋅exp(n)), where n = O(log(N)) is the inner block length. In other words, it is NO(1) (i.e., polynomial-time) in terms of the outer block length N. As the outer decoding algorithm in step two is assumed to run in polynomial time the complexity of the overall decoding algorithm is polynomial-time as well.
' with less than D/2 symbols y' i in error. Similarly, the inner code can reliably correct an input yi if less than d/2 inner symbols are erroneous. Thus, for an outer symbol y' i to be incorrect after inner decoding at least d/2 inner symbols must have been in error, and for the outer code to fail this must have happened for at least D/2 outer symbols. Consequently, the total number of inner symbols that must be received incorrectly for the concatenated code to fail must be at least d/2⋅D/2 = dD/4.
The algorithm also works if the inner codes are different, e.g., for Justesen codes. The generalized minimum distance algorithm
, developed by Forney, can be used to correct up to dD/2 errors.
It uses erasure
information from the inner code to improve performance of the outer code, and was the first example of an algorithm using soft-decision decoding.
communication with the Voyager program
, which launched their first probe in 1977. Since then, concatenated codes became the workhorse for efficient error correction coding, and stayed so at least until the invention of turbo codes and LDPC codes.
Typically, the inner code is not a block code but a soft-decision
convolutional
Viterbi-decoded
code with a short constraint length.
For the outer code, a longer hard-decision block code, frequently Reed Solomon with 8-bit symbols, is selected.
The larger symbol size makes the outer code more robust to burst error
s that may occur due to channel impairments, and because erroneous output of the convolutional code itself is bursty. An interleaving
layer is usually added between the two codes to spread burst errors across a wider range.
The combination of an inner Viterbi convolutional code with an outer Reed-Solomon code (known as an RSV code) was first used on Voyager 2
, and became a popular construction both within and outside of the space sector. It is still notably used today for satellite communication, such as the DVB-S
digital television
broadcast standard.
In a more loose sense, any (serial) combination of two or more codes may be referred to as a concatenated code. For example, within the DVB-S2
standard, a highly efficient LDPC code is combined with an algebraic outer code in order to remove any resilient errors left over from the inner LDPC code due to its inherent error floor
.
A simple concatenation scheme is also used on the Compact Disc
, where an interleaving layer between two Reed-Solomon codes of different sizes effectively spreads errors across different blocks.
s, as described first in 1993, implemented a parallel concatenation of two convolutional codes, with an interleaver between the two codes and an iterative decoder that would pass information forth and back between the codes. This construction had much higher performance than all previously conceived concatenated codes.
However, a key aspect of turbo codes is their iterated decoding approach. Iterated decoding is now also applied to serial concatenations in order to achieve higher coding gains, such as within serially concatenated convolutional codes (SCCCs). An early form of iterated decoding was notably implemented with 2 to 5 iterations in the "Galileo code" of the Galileo spacecraft.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
.
Concatenated codes became widely used in space communications in the 1970s.
Background
The field of channel coding is concerned with sending a stream of data at the highest possible rate over a given communications channel, and then decoding the original data reliably at the receiver, using encoding and decoding algorithms that are feasible to implement in a given technology.Shannon's channel coding theorem shows that over many common channels there exist channel coding schemes that are able to transmit data reliably at all rates
 less than a certain threshold
less than a certain threshold  , called the channel capacity
, called the channel capacityChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
of the given channel. In fact, the probability of decoding error can be made to decrease exponentially as the block length
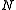 of the coding scheme goes to infinity. However, the complexity of a naive optimum decoding scheme that simply computes the likelihood of every possible transmitted codeword increases exponentially with
of the coding scheme goes to infinity. However, the complexity of a naive optimum decoding scheme that simply computes the likelihood of every possible transmitted codeword increases exponentially with 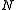 , so such an optimum decoder rapidly becomes infeasible.
, so such an optimum decoder rapidly becomes infeasible.In his doctoral thesis, Dave Forney showed that concatenated codes could be used to achieve exponentially decreasing error probabilities at all data rates less than capacity, with decoding complexity that increases only polynomially with the code block length.
Description
Let Cin be a [n, k, d] code, that is, a block codeBlock code
In coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
of length n, dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
k, minimum Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
d, and rate
Code rate
In telecommunication and information theory, the code rate of a forward error correction code is the proportion of the data-stream that is useful...
r = n/k, over an alphabet A:

Let Cout be a [N, K, D] code over an alphabet B with |B| = |A|k symbols:
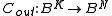
The inner code Cin takes one of |A|k = |B| possible inputs, encodes into an n-tuple over A, transmits, and decodes into one of |B| possible outputs. We regard this as a (super) channel which can transmit one symbol from the alphabet B. We use this channel N times to transmit each of the N symbols in a codeword of Cout. The concatenation of Cout (as outer code) with Cin (as inner code), denoted Cout∘Cin, is thus a code of length Nn over the alphabet A:
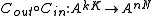
It maps each input message m = (m1, m2, ..., mK) to a codeword (Cin(m
where (m
The key insight in this approach is that if Cin is decoded using a maximum-likelihood approach (thus showing an exponentially decreasing error probability with increasing length), and Cout is a code with length N = 2nr that can be decoded in polynomial time of N, then the concatenated code can be decoded in polynomial time of its combined length n2nr = O(N⋅log(N)) and shows an exponentially decreasing error probability, even if Cin has exponential decoding complexity. This is discussed in more detail in section Decoding concatenated codes.
In a generalization of above concatenation, there are N possible inner codes Cin,i and the i-th symbol in a codeword of Cout is transmitted across the inner channel using the i-th inner code. The Justesen codes are examples of generalized concatenated codes, where the outer code is a Reed-Solomon code.
Properties
1. The distance of the concatenated code Cout∘Cin is at least dD, that is, it is a [nN, kK, DProof:
Consider two different messages m1 ≠ m2 ∈ BK. Let Δ denote the distance between two codewords. Then
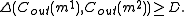
Thus, there are at least D positions in which the sequence of N symbols of the codewords Cout(m1) and Cout(m2) differ. For these positions, denoted i, we have

Consequently, there are at least d⋅D positions in the sequence of n⋅N symbols taken from the alphabet A in which the two codewords differ, and hence
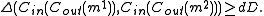
2. If Cout and Cin are linear block codes, then Cout∘Cin is also a linear block code.
This property can be easily shown based on the idea of defining a generator matrix
Generator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
for the concatenated code in terms of the generator matrices of Cout and Cin.
Decoding concatenated codes
A natural concept for a decoding algorithm for concatenated codes is to first decode the inner code and then the outer code. For the algorithm to be practical it must be polynomial-time in the final block length. Consider that there is a polynomial-time unique decoding algorithm for the outer code. Now we have to find a polynomial-time decoding algorithm for the inner code. It is understood that polynomial running time here means that running time is polynomial in the final block length. The main idea is that if the inner block length is selected to be logarithmic in the size of the outer code then the decoding algorithm for the inner code may run in exponential time of the inner block length, and we can thus use an exponential-time but optimal maximum likelihood decoder (MLD) for the inner code.In detail, let the input to the decoder be the vector y = (y1, ..., yN) ∈ (An)N. Then the decoding algorithm is a two-step process:
- Use the MLD of the inner code Cin to reconstruct a set of inner code words y
' = (y' 1, ..., y' N), with y' i = MLDCin(yi), 1 ≤ i ≤ N. - Run the unique decoding algorithm for Cout on y
' .
Now, the time complexity of the first step is O(N⋅exp(n)), where n = O(log(N)) is the inner block length. In other words, it is NO(1) (i.e., polynomial-time) in terms of the outer block length N. As the outer decoding algorithm in step two is assumed to run in polynomial time the complexity of the overall decoding algorithm is polynomial-time as well.
Remarks
The decoding algorithm described above can be used to correct all errors up to less than dD/4 in number. Using minimum distance decoding, the outer decoder can correct all inputs yThe algorithm also works if the inner codes are different, e.g., for Justesen codes. The generalized minimum distance algorithm
Generalized minimum distance decoding
In coding theory, generalized minimum-distance decoding provides an efficient algorithm for decoding concatenated codes, which is based on using an errors-and-erasures decoder for the outer code....
, developed by Forney, can be used to correct up to dD/2 errors.
It uses erasure
Erasure code
In information theory, an erasure code is a forward error correction code for the binary erasure channel, which transforms a message of k symbols into a longer message with n symbols such that the original message can be recovered from a subset of the n symbols...
information from the inner code to improve performance of the outer code, and was the first example of an algorithm using soft-decision decoding.
Applications
Although a simple concatenation scheme was implemented already for the 1971 Mariner Mars orbiter mission, concatenated codes were starting to be regularly used for deep spaceDeep Space
- Star Trek :* Battle of Deep Space Nine, the first major battle of the Dominion War* Deep Space Nine , space station in the fictional Star Trek universe* Deep Space Nine relaunch, number of novels released since 2000...
communication with the Voyager program
Voyager program
The Voyager program is a U.S program that launched two unmanned space missions, scientific probes Voyager 1 and Voyager 2. They were launched in 1977 to take advantage of a favorable planetary alignment of the late 1970s...
, which launched their first probe in 1977. Since then, concatenated codes became the workhorse for efficient error correction coding, and stayed so at least until the invention of turbo codes and LDPC codes.
Typically, the inner code is not a block code but a soft-decision
Soft-decision decoder
In information theory, a soft-decision decoder is a class of algorithm used to decode data that has been encoded with an error correcting code. Whereas a hard-decision decoder operates on data that take on a fixed set of possible values , the inputs to a soft-decision decoder may take on a whole...
convolutional
Convolutional code
In telecommunication, a convolutional code is a type of error-correcting code in which* each m-bit information symbol to be encoded is transformed into an n-bit symbol, where m/n is the code rate and...
Viterbi-decoded
Viterbi decoder
A Viterbi decoder uses the Viterbi algorithm for decoding a bitstream that has beenencoded using forward error correction based on a convolutional code....
code with a short constraint length.
For the outer code, a longer hard-decision block code, frequently Reed Solomon with 8-bit symbols, is selected.
The larger symbol size makes the outer code more robust to burst error
Error burst
In telecommunication, a burst error or error burst is a contiguous sequence of symbols, received over a data transmission channel, such that the first and last symbols are in error and there exists no contiguous subsequence of m correctly received symbols within the error burst.The integer...
s that may occur due to channel impairments, and because erroneous output of the convolutional code itself is bursty. An interleaving
Interleaving
In computer science and telecommunication, interleaving is a way to arrange data in a non-contiguous way to increase performance.It is typically used:* In error-correction coding, particularly within data transmission, disk storage, and computer memory....
layer is usually added between the two codes to spread burst errors across a wider range.
The combination of an inner Viterbi convolutional code with an outer Reed-Solomon code (known as an RSV code) was first used on Voyager 2
Voyager 2
The Voyager 2 spacecraft is a 722-kilogram space probe launched by NASA on August 20, 1977 to study the outer Solar System and eventually interstellar space...
, and became a popular construction both within and outside of the space sector. It is still notably used today for satellite communication, such as the DVB-S
DVB-S
DVB-S is an abbreviation for Digital Video Broadcasting — Satellite; it is the original Digital Video Broadcasting forward error coding and demodulation standard for satellite television and dates from 1994, in its first release, while development lasted from 1993 to 1997...
digital television
Digital television
Digital television is the transmission of audio and video by digital signals, in contrast to the analog signals used by analog TV...
broadcast standard.
In a more loose sense, any (serial) combination of two or more codes may be referred to as a concatenated code. For example, within the DVB-S2
DVB-S2
Digital Video Broadcasting - Satellite - Second Generation is a digital television broadcast standard that has been designed as a successor for the popular DVB-S system. It was developed in 2003 by the , an international industry consortium, and ratified by ETSI in March 2005...
standard, a highly efficient LDPC code is combined with an algebraic outer code in order to remove any resilient errors left over from the inner LDPC code due to its inherent error floor
Error floor
The error floor is a phenomenon encountered in modern iterated sparse graph-based error correcting codes like LDPC codes and turbo codes. When the bit error ratio curve is plotted for conventional codes like Reed Solomon codes under algebraic decoding or for convolutional codes under Viterbi...
.
A simple concatenation scheme is also used on the Compact Disc
Compact Disc
The Compact Disc is an optical disc used to store digital data. It was originally developed to store and playback sound recordings exclusively, but later expanded to encompass data storage , write-once audio and data storage , rewritable media , Video Compact Discs , Super Video Compact Discs ,...
, where an interleaving layer between two Reed-Solomon codes of different sizes effectively spreads errors across different blocks.
Turbo codes: A parallel concatenation approach
The description above is given for what is now called a serially concatenated code. Turbo codeTurbo code
In information theory, turbo codes are a class of high-performance forward error correction codes developed in 1993, which were the first practical codes to closely approach the channel capacity, a theoretical maximum for the code rate at which reliable communication is still possible given a...
s, as described first in 1993, implemented a parallel concatenation of two convolutional codes, with an interleaver between the two codes and an iterative decoder that would pass information forth and back between the codes. This construction had much higher performance than all previously conceived concatenated codes.
However, a key aspect of turbo codes is their iterated decoding approach. Iterated decoding is now also applied to serial concatenations in order to achieve higher coding gains, such as within serially concatenated convolutional codes (SCCCs). An early form of iterated decoding was notably implemented with 2 to 5 iterations in the "Galileo code" of the Galileo spacecraft.

