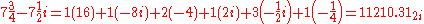Quater-imaginary base
Encyclopedia
The quater-imaginary numeral system
was first proposed by Donald Knuth
in 1955, in a submission to a high-school science talent search. It is a non-standard positional numeral system
which uses the imaginary number
2i as its base. It is able to (almost) uniquely represent every complex number
using only the digits 0, 1, 2, and 3. (Numbers less than zero, which are ordinarily represented with a minus sign, are representable as digit strings in quater-imaginary; for example, the number −1 is represented as "103" in quater-imaginary notation.)
in base b can be converted to a decimal number using the formula
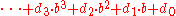
For the quater-imaginary system,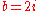
.
to a decimal number, fill in the formula above:
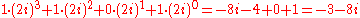
Another, longer example:
in base 10 is
(every number of the form a+bi) has a quater-imaginary representation. Most numbers have a unique quater-imaginary representation, but just as 1 has the two representations 1.0 = 0.9...
in decimal notation, so 1/5 has the two quater-imaginary representations 1.(0300)…2i = 0.(0003)…2i.
To convert an arbitrary complex number to quater-imaginary, it is sufficient to split the number into its real and imaginary components, convert each of those separately, and then add the results by interleaving the digits. For example, since –1+4i is equal to –1 plus 4i, the quater-imaginary representation of –1+4i is the quater-imaginary representation of –1 (namely, 103) plus the quater-imaginary representation of 4i (namely, 20), which gives a final result of –1+4i = 1232i.
To find the quater-imaginary representation of the imaginary component, it suffices to multiply that component by 2i, which gives a real number; then find the quater-imaginary representation of that real number, and finally shift the representation by one place to the right (thus dividing by 2i). For example, the quater-imaginary representation of 6i is calculated by multiplying 6i • 2i = –12, which is expressed as 3002i, and then shifting by one place to the right, yielding: 6i = 302i.
Finding the quater-imaginary representation of an arbitrary real number can be done manually by solving a system of simultaneous equations
, as shown below.
To find the representation, first write out the general formula, and group terms: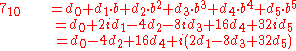
Since 7 is a real number, it is allowed to conclude that d1, d3 and d5 should be zero. Now the value of the coefficients d0, d2 and d4, must be found. Because d0 − 4 d2 + 16 d4 = 7 and because—by the nature of the quater-imaginary system—the coefficients can only be 0, 1, 2 or 3 the value of the coefficients can be found. A possible configuration could be: d0 = 3, d2 = 3 and d4 = 1. This configuration gives the resulting digit string for 710.
in the decimal system is the usual . (dot) which marks the separation between the integral
part and the fraction
al part of the number.
In the quater-imaginary system a radix point can also be used. For a digit string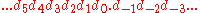
the radix point marks the separation between positive and negative powers of b. Using the radix point the general formula becomes:
or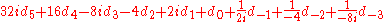
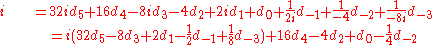
For certain coefficients dk. Then because the real part has to be zero: d4 = d2 = d0 = d-2 = 0.
For the imaginary part, if d5 = d3 = d -3 = 0 and when d1=1 and d-1=2 the digit string can be found. Using the above coefficients in the digit string the result is:
.
and subtract
numbers in the quater-imaginary system. In doing this, there are two basic rules that have to be kept in mind:
Or for short: "If you add four, carry +1. If you subtract four, carry -1". This is the opposite of normal long addition, in which a "carry" in the current column requires adding 1 to the next column to the left, and a "borrow" requires subtracting. In quater-imaginary arithmetic, a "carry" subtracts from the next-but-one column, and a "borrow" adds.
1 - 2i 1031 3 - 4i 1023
1 - 2i 1031 1 - 8i 1001
------- + <=> ----- + ------- + <=> ----- +
2 - 4i 1022 4 - 12i 12320
In the first example we start by adding the two 1s in the first column (the "ones' column"), giving 2. Then we add the two 3s in the second column (the "2is column"), giving 6; 6 is greater than 3, so we subtract 4 (giving 2 as the result in the second column) and carry −1 into the fourth column. Adding the 0s in the third column gives 0; and finally adding the two 1s and the carried −1 in the fourth column gives 1.
In the second example we first add 3+1, giving 4; 4 is greater than 3, so we subtract 4 (giving 0) and carry −1 into the third column (the "−4s column"). Then we add 2+0 in the second column, giving 2. In the third column, we have 0+0+(−1), because of the carry; −1 is less than 0, so we add 4 (giving 3 as the result in the third column) and "borrow" +1 into the fifth column. In the fourth column, 1+1 is 2; and the carry in the fifth column gives 1, for a result of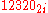
.
- 2 - 8i 1102
1 - 6i 1011
------- - <=> ----- -
- 3 - 2i 1131
In this example we have to subtract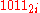
from 
. The rightmost digit is 2−1 = 1. The second digit from the right would become −1, so add 4 to give 3 and then carry +1 two places to the left. The third digit from the right is 1−0 = 1. Then the leftmost digit is 1−1 plus 1 from the carry, giving 1. This gives a final answer of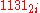 
.
Then the resulting partial products are added where each is shifted to the left by one digit. An example:
11201
20121 x
--------
11201 <--- 1 x 11201
12002 <--- 2 x 11201
11201 <--- 1 x 11201
00000 <--- 0 x 11201
12002 + <--- 2 x 11201
------------
120231321
This corresponds to a multiplication of
.
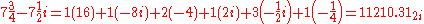
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
was first proposed by Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in 1955, in a submission to a high-school science talent search. It is a non-standard positional numeral system
Non-standard positional numeral systems
Non-standard positional numeral systems here designates numeral systems that may be denoted positional systems, but that deviate in one way or another from the following description of standard positional systems:...
which uses the imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
2i as its base. It is able to (almost) uniquely represent every complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
using only the digits 0, 1, 2, and 3. (Numbers less than zero, which are ordinarily represented with a minus sign, are representable as digit strings in quater-imaginary; for example, the number −1 is represented as "103" in quater-imaginary notation.)
Converting from quater-imaginary
To convert a digit string from the quater-imaginary system to the decimal system, the standard formula for positional number systems can be used. This says that a digit string in base b can be converted to a decimal number using the formula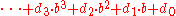For the quater-imaginary system,
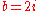.Example
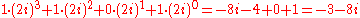
To convert the string to a decimal number, fill in the formula above:Another, longer example:
in base 10 isConverting into quater-imaginary
It is also possible to convert a decimal number to a number in the quater-imaginary system. Every complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
(every number of the form a+bi) has a quater-imaginary representation. Most numbers have a unique quater-imaginary representation, but just as 1 has the two representations 1.0 = 0.9...
0.999...
In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number...
in decimal notation, so 1/5 has the two quater-imaginary representations 1.(0300)…2i = 0.(0003)…2i.
To convert an arbitrary complex number to quater-imaginary, it is sufficient to split the number into its real and imaginary components, convert each of those separately, and then add the results by interleaving the digits. For example, since –1+4i is equal to –1 plus 4i, the quater-imaginary representation of –1+4i is the quater-imaginary representation of –1 (namely, 103) plus the quater-imaginary representation of 4i (namely, 20), which gives a final result of –1+4i = 1232i.
To find the quater-imaginary representation of the imaginary component, it suffices to multiply that component by 2i, which gives a real number; then find the quater-imaginary representation of that real number, and finally shift the representation by one place to the right (thus dividing by 2i). For example, the quater-imaginary representation of 6i is calculated by multiplying 6i • 2i = –12, which is expressed as 3002i, and then shifting by one place to the right, yielding: 6i = 302i.
Finding the quater-imaginary representation of an arbitrary real number can be done manually by solving a system of simultaneous equations
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
, as shown below.
Example: Real number
As an example of a real number we can try to find the quater-imaginary counterpart of the decimal number 7 (or 710 since the base of the decimal system is 10). Since it is hard to predict exactly how long the digit string will be for a given decimal number, it is safe to assume a fairly large string. In this case, a string of six digits can be chosen. When an initial guess at the size of the string eventually turns out to be insufficient, a larger string can be used.To find the representation, first write out the general formula, and group terms:
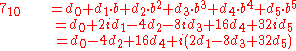
Since 7 is a real number, it is allowed to conclude that d1, d3 and d5 should be zero. Now the value of the coefficients d0, d2 and d4, must be found. Because d0 − 4 d2 + 16 d4 = 7 and because—by the nature of the quater-imaginary system—the coefficients can only be 0, 1, 2 or 3 the value of the coefficients can be found. A possible configuration could be: d0 = 3, d2 = 3 and d4 = 1. This configuration gives the resulting digit string for 710.
Example: Imaginary number
Finding a quater-imaginary representation of a purely complex number is analogous to the method described above for a real number. For example, to find the representation of 6i, it is possible to use the general formula. Then all coefficients of the real part have to be zero and the complex part should make 6. However, for 6i it is easily seen by looking at the formula that if d1 = 3 and all other coefficients are zero, we get the desired string for 6i. That is:Radix point "."
A radix pointRadix point
In mathematics and computing, a radix point is the symbol used in numerical representations to separate the integer part of a number from its fractional part . "Radix point" is a general term that applies to all number bases...
in the decimal system is the usual . (dot) which marks the separation between the integral
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
part and the fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
al part of the number.
In the quater-imaginary system a radix point can also be used. For a digit string
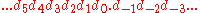the radix point marks the separation between positive and negative powers of b. Using the radix point the general formula becomes:or
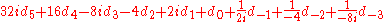
Example
If the quater-imaginary representation of the complex unit i has to be found, the formula without radix point will not suffice. Therefore the above formula should be used. Hence: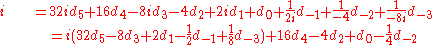For certain coefficients dk. Then because the real part has to be zero: d4 = d2 = d0 = d-2 = 0.
For the imaginary part, if d5 = d3 = d -3 = 0 and when d1=1 and d-1=2 the digit string can be found. Using the above coefficients in the digit string the result is:
.Addition and subtraction
It is possible to addAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and subtract
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
numbers in the quater-imaginary system. In doing this, there are two basic rules that have to be kept in mind:
- Whenever a number exceeds 3, subtract 4 and "carry" −1 two places to the left.
- Whenever a number drops below 0, add 4 and "carry" +1 two places to the left.
Or for short: "If you add four, carry +1. If you subtract four, carry -1". This is the opposite of normal long addition, in which a "carry" in the current column requires adding 1 to the next column to the left, and a "borrow" requires subtracting. In quater-imaginary arithmetic, a "carry" subtracts from the next-but-one column, and a "borrow" adds.
Example: Addition
Below are two examples of adding in the quater-imaginary system:1 - 2i 1031 3 - 4i 1023
1 - 2i 1031 1 - 8i 1001
------- + <=> ----- + ------- + <=> ----- +
2 - 4i 1022 4 - 12i 12320
In the first example we start by adding the two 1s in the first column (the "ones' column"), giving 2. Then we add the two 3s in the second column (the "2is column"), giving 6; 6 is greater than 3, so we subtract 4 (giving 2 as the result in the second column) and carry −1 into the fourth column. Adding the 0s in the third column gives 0; and finally adding the two 1s and the carried −1 in the fourth column gives 1.
In the second example we first add 3+1, giving 4; 4 is greater than 3, so we subtract 4 (giving 0) and carry −1 into the third column (the "−4s column"). Then we add 2+0 in the second column, giving 2. In the third column, we have 0+0+(−1), because of the carry; −1 is less than 0, so we add 4 (giving 3 as the result in the third column) and "borrow" +1 into the fifth column. In the fourth column, 1+1 is 2; and the carry in the fifth column gives 1, for a result of
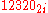.Example: Subtraction
Subtraction is analogous to addition in that it uses the same two rules described above. Below is an example:- 2 - 8i 1102
1 - 6i 1011
------- - <=> ----- -
- 3 - 2i 1131
In this example we have to subtract
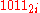from . The rightmost digit is 2−1 = 1. The second digit from the right would become −1, so add 4 to give 3 and then carry +1 two places to the left. The third digit from the right is 1−0 = 1. Then the leftmost digit is 1−1 plus 1 from the carry, giving 1. This gives a final answer of 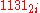.Multiplication
For long multiplication in the quater-imaginary system, the two rules stated above are used as well. When multiplying numbers, multiply the first string by each digit in the second string consecutively and add the resulting strings. With every multiplication, a digit in the second string is multiplied with the first string. The multiplication starts with the rightmost digit in the second string and then moves leftward by one digit, multiplying each digit with the first string.Then the resulting partial products are added where each is shifted to the left by one digit. An example:
11201
20121 x
--------
11201 <--- 1 x 11201
12002 <--- 2 x 11201
11201 <--- 1 x 11201
00000 <--- 0 x 11201
12002 + <--- 2 x 11201
------------
120231321
This corresponds to a multiplication of
.Tabulated conversions
Below is a table of some decimal and complex numbers and their quater-imaginary counterparts.| Base 10 | Base 2i |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 10300 |
| 5 | 10301 |
| 6 | 10302 |
| 7 | 10303 |
| 8 | 10200 |
| 9 | 10201 |
| 10 | 10202 |
| 11 | 10203 |
| 12 | 10100 |
| 13 | 10101 |
| 14 | 10102 |
| 15 | 10103 |
| 16 | 10000 |
| Base 10 | Base 2i |
|---|---|
| −1 | 103 |
| −2 | 102 |
| −3 | 101 |
| −4 | 100 |
| −5 | 203 |
| −6 | 202 |
| −7 | 201 |
| −8 | 200 |
| −9 | 303 |
| −10 | 302 |
| −11 | 301 |
| −12 | 300 |
| −13 | 1030003 |
| −14 | 1030002 |
| −15 | 1030001 |
| −16 | 1030000 |
| Base 10 | Base 2i |
|---|---|
| 1i | 10.2 |
| 2i | 10.0 |
| 3i | 20.2 |
| 4i | 20.0 |
| 5i | 30.2 |
| 6i | 30.0 |
| 7i | 103000.2 |
| 8i | 103000.0 |
| 9i | 103010.2 |
| 10i | 103010.0 |
| 11i | 103020.2 |
| 12i | 103020.0 |
| 13i | 103030.2 |
| 14i | 103030.0 |
| 15i | 102000.2 |
| 16i | 102000.0 |
| Base 10 | Base 2i |
|---|---|
| −1i | 0.2 |
| −2i | 1030.0 |
| −3i | 1030.2 |
| −4i | 1020.0 |
| −5i | 1020.2 |
| −6i | 1010.0 |
| −7i | 1010.2 |
| −8i | 1000.0 |
| −9i | 1000.2 |
| −10i | 2030.0 |
| −11i | 2030.2 |
| −12i | 2020.0 |
| −13i | 2020.2 |
| −14i | 2010.0 |
| −15i | 2010.2 |
| −16i | 2000.0 |
Examples
Below are some other examples of conversions from decimal numbers to quater-imaginary numbers.