
Enumerative combinatorics
Encyclopedia
Enumerative combinatorics is an area of combinatorics
that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations. More generally, given an infinite collection of finite sets {Si} indexed by the natural number
s, enumerative combinatorics seeks to describe a counting function which counts the number of objects in Sn for each n. Although counting the number of elements in a set is a rather broad mathematical problem
, many of the problems that arise in applications have a relatively simple combinatorial description. The twelvefold way
provides a unified framework for counting permutations, combinations and partitions
.
The simplest such functions are closed formulas, which can be expressed as a composition of elementary functions such as factorial
s, powers, and so on. For instance, as shown below, the number of different possible orderings of a deck of n cards is f(n) = n!. Often, no closed form is initially available. In these cases, we frequently first derive a recurrence relation
, then solve the recurrence to arrive at the desired closed form.
Finally, f(n) may be expressed by a formal power series
, called its generating function
, which is most commonly either the ordinary generating function
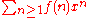
or the exponential generating function
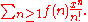
Often, a complicated closed formula yields little insight into the behavior of the counting function as the number of counted objects grows.
In these cases, a simple asymptotic
approximation may be preferable. A function is an asymptotic approximation to
is an asymptotic approximation to 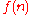 if
if 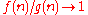 as
as  . In this case, we write
. In this case, we write 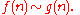
Once determined, the generating function may allow one to extract all the information given by the previous approaches. In addition, the various natural operations on generating functions such as addition, multiplication, differentiation, etc., have a combinatorial significance; this allows one to extend results from one combinatorial problem in order to solve others.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations. More generally, given an infinite collection of finite sets {Si} indexed by the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, enumerative combinatorics seeks to describe a counting function which counts the number of objects in Sn for each n. Although counting the number of elements in a set is a rather broad mathematical problem
Mathematical problem
A mathematical problem is a problem that is amenable to being represented, analyzed, and possibly solved, with the methods of mathematics. This can be a real-world problem, such as computing the orbits of the planets in the solar system, or a problem of a more abstract nature, such as Hilbert's...
, many of the problems that arise in applications have a relatively simple combinatorial description. The twelvefold way
Twelvefold way
In combinatorics, the twelvefold way is a name given to a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number...
provides a unified framework for counting permutations, combinations and partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
.
The simplest such functions are closed formulas, which can be expressed as a composition of elementary functions such as factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s, powers, and so on. For instance, as shown below, the number of different possible orderings of a deck of n cards is f(n) = n!. Often, no closed form is initially available. In these cases, we frequently first derive a recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
, then solve the recurrence to arrive at the desired closed form.
Finally, f(n) may be expressed by a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
, called its generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
, which is most commonly either the ordinary generating function
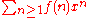
or the exponential generating function
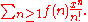
Often, a complicated closed formula yields little insight into the behavior of the counting function as the number of counted objects grows.
In these cases, a simple asymptotic
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
approximation may be preferable. A function
 is an asymptotic approximation to
is an asymptotic approximation to 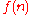 if
if 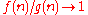 as
as  . In this case, we write
. In this case, we write 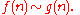
Once determined, the generating function may allow one to extract all the information given by the previous approaches. In addition, the various natural operations on generating functions such as addition, multiplication, differentiation, etc., have a combinatorial significance; this allows one to extend results from one combinatorial problem in order to solve others.
See also
- Combinatorial principlesCombinatorial principlesIn proving results in combinatorics several useful combinatorial rules or combinatorial principles are commonly recognized and used.The rule of sum, rule of product, and inclusion-exclusion principle are often used for enumerative purposes. Bijective proofs are utilized to demonstrate that two sets...
- Fundamental theorem of combinatorial enumerationFundamental theorem of combinatorial enumerationThe fundamental theorem of combinatorial enumeration is a theorem in combinatorics that solves the enumeration problem of labelled and unlabelled combinatorial classes.The unlabelled case is based on the Pólya enumeration theorem....
- Algebraic combinatoricsAlgebraic combinatoricsAlgebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
- Asymptotic combinatorics
- Combinatorial explosionCombinatorial explosionIn administration and computing, a combinatorial explosion is the rapidly accelerating increase in lines of communication as organizations are added in a process...
- Inclusion-exclusion principleInclusion-exclusion principleIn combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
- Method of distinguished elementMethod of distinguished elementIn enumerative combinatorial mathematics, identities are sometimes established by arguments that rely on singling out one "distinguished element" of a set.-Examples:...
- Combinatorial speciesCombinatorial speciesIn combinatorial mathematics, the theory of combinatorial species is an abstract, systematic method for analysing discrete structures in terms of generating functions. Examples of discrete structures are graphs, permutations, trees, and so on; each of these has an associated generating function...
- Sieve theorySieve theorySieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
- Pólya enumeration theoremPólya enumeration theoremThe Pólya enumeration theorem , also known as the Redfield–Pólya Theorem, is a theorem in combinatorics that both follows and ultimately generalizes Burnside's lemma on the number of orbits of a group action on a set. The theorem was first published by John Howard Redfield in 1927...

