Clustering high-dimensional data
Encyclopedia
Clustering high-dimensional data is the cluster analysis of data with anywhere from a few dozen to many thousands of dimension
s. Such high-dimensional data spaces are often encountered in areas such as medicine, where DNA microarray
technology can produce a large number of measurements at once, and the clustering of text documents, where, if a word-frequency vector is used, the number of dimensions equals the size of the dictionary.
Recent research by indicates that the discrimination problems only occur when there is a high number of irrelevant dimensions, and that shared-nearest-neighbor approaches can improve results.
in the data matrix, often referred to as biclustering
, which is a technique frequently utilized in bioinformatics
.
 Subspace clustering is the task of detecting all clusters in all subspaces. This means that a point might be a member of multiple clusters, each existing in a different subspace. Subspaces can either be axis-parallel or affine. The term is often used synonymous with general clustering in high-dimensional data.
Subspace clustering is the task of detecting all clusters in all subspaces. This means that a point might be a member of multiple clusters, each existing in a different subspace. Subspaces can either be axis-parallel or affine. The term is often used synonymous with general clustering in high-dimensional data.
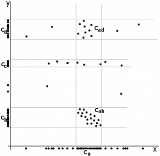
The image on the right shows a mere two-dimensional space where a number of clusters can be identified. In the one-dimensional subspaces, the clusters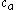 (in subspace
(in subspace 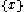 ) and
) and 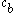 ,
, 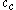 ,
, 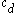 (in subspace
(in subspace 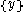 ) can be found.
) can be found. 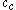 cannot be considered a cluster in a two-dimensional (sub-)space, since it is too sparsely distributed in the
cannot be considered a cluster in a two-dimensional (sub-)space, since it is too sparsely distributed in the  axis. In two dimensions, the two clusters
axis. In two dimensions, the two clusters 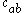 and
and  can be identified.
can be identified.
The problem of subspace clustering is given by the fact that there are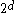 different subspaces of a space with
different subspaces of a space with 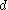 dimensions. If the subspaces are not axis-parallel, an infinite number of subspaces is possible. Hence, subspace clustering algorithm utilize some kind of heuristic
dimensions. If the subspaces are not axis-parallel, an infinite number of subspaces is possible. Hence, subspace clustering algorithm utilize some kind of heuristic
to remain computationally feasible, at the risk of producing inferior results. For example, the downward-closure property (cf. association rules
) can be used to build higher-dimensional subspaces only by combining lower-dimensional ones, as any subspace T containing a cluster, will result in a full space S also to contain that cluster (i.e. S ⊆ T), an approach taken by most of the traditional algorithms such as CLIQUE and SUBCLU
.
For example, the PreDeCon algorithm checks which attributes seem to support a clustering for each point, and adjusts the distance function such that dimensions with low variance
are amplified in the distance function . In the figure above, the cluster might be found using DBSCAN
might be found using DBSCAN
with a distance function that places less emphasis on the -axis and thus exaggerates the low difference in the
-axis and thus exaggerates the low difference in the 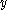 -axis sufficiently enough to group the points into a cluster.
-axis sufficiently enough to group the points into a cluster.
PROCLUS uses a similar approach with a k-medoid clustering . Initial medoids are guessed, and for each medoid the subspace spanned by attributes with low variance is determined. Points are assigned to the medoid closest, considering only the subspace of that medoid in determining the distance. The algorithm then proceeds as the regular PAM algorithm.
If the distance function weights attributes differently, but never with 0 (and hence never drops irrelevant attributes), the algorithm is called a "soft"-projected clustering algorithm.
too aggressive to credibly produce all subspace clusters .
.
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s. Such high-dimensional data spaces are often encountered in areas such as medicine, where DNA microarray
DNA microarray
A DNA microarray is a collection of microscopic DNA spots attached to a solid surface. Scientists use DNA microarrays to measure the expression levels of large numbers of genes simultaneously or to genotype multiple regions of a genome...
technology can produce a large number of measurements at once, and the clustering of text documents, where, if a word-frequency vector is used, the number of dimensions equals the size of the dictionary.
Problems
According to , four problems need to be overcome for clustering in high-dimensional data:- Multiple dimensions are hard to think in, impossible to visualize, and, due to the exponential growth of the number of possible values with each dimension, impossible to enumerate. This problem is known as the curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
. - The concept of distance becomes less precise as the number of dimensions grows, since the distance between any two points in a given dataset converges. The discrimination of the nearest and farthest point in particular becomes meaningless:
-
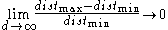
- A cluster is intended to group objects that are related, based on observations of their attribute's values. However, given a large number of attributes some of the attributes will usually not be meaningful for a given cluster. For example, in newborn screeningNewborn screeningNewborn screening is the process by which infants are screened shortly after birth for a list of disorders that are treatable, but difficult or impossible to detect clinically. Screening programs are often run by state or national governing bodies with the goal of screening all infants born in the...
a cluster of samples might identify newborns that share similar blood values, which might lead to insights about the relevance of certain blood values for a disease. But for different diseases, different blood values might form a cluster, and other values might be uncorrelated. This is known as the local feature relevance problem: different clusters might be found in different subspaces, so a global filtering of attributes is not sufficient. - Given a large number of attributes, it is likely that some attributes are correlated. Hence, clusters might exist in arbitrarily oriented affine subspaces.
- A cluster is intended to group objects that are related, based on observations of their attribute's values. However, given a large number of attributes some of the attributes will usually not be meaningful for a given cluster. For example, in newborn screening
Recent research by indicates that the discrimination problems only occur when there is a high number of irrelevant dimensions, and that shared-nearest-neighbor approaches can improve results.
Approaches
Approaches towards clustering in axis-parallel or arbitrarily oriented affine subspaces differ in how they interpret the overall goal, which is finding clusters in data with high dimensionality. This distinction is proposed in . An overall different approach is to find clusters based on patternPattern
A pattern, from the French patron, is a type of theme of recurring events or objects, sometimes referred to as elements of a set of objects.These elements repeat in a predictable manner...
in the data matrix, often referred to as biclustering
Biclustering
Biclustering, co-clustering, or two-mode clustering is a data mining technique which allows simultaneous clustering of the rows and columns of a matrix....
, which is a technique frequently utilized in bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
.
Subspace Clustering

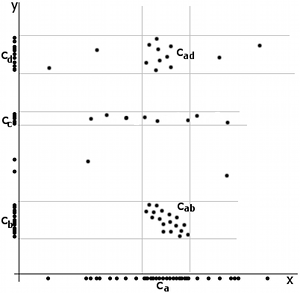
The image on the right shows a mere two-dimensional space where a number of clusters can be identified. In the one-dimensional subspaces, the clusters
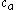 (in subspace
(in subspace 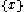 ) and
) and 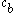 ,
, 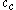 ,
, 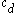 (in subspace
(in subspace 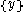 ) can be found.
) can be found. 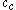 cannot be considered a cluster in a two-dimensional (sub-)space, since it is too sparsely distributed in the
cannot be considered a cluster in a two-dimensional (sub-)space, since it is too sparsely distributed in the  axis. In two dimensions, the two clusters
axis. In two dimensions, the two clusters 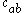 and
and  can be identified.
can be identified.The problem of subspace clustering is given by the fact that there are
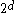 different subspaces of a space with
different subspaces of a space with 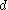 dimensions. If the subspaces are not axis-parallel, an infinite number of subspaces is possible. Hence, subspace clustering algorithm utilize some kind of heuristic
dimensions. If the subspaces are not axis-parallel, an infinite number of subspaces is possible. Hence, subspace clustering algorithm utilize some kind of heuristicHeuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
to remain computationally feasible, at the risk of producing inferior results. For example, the downward-closure property (cf. association rules
Association rule learning
In data mining, association rule learning is a popular andwell researched method for discovering interesting relations between variablesin large databases. Piatetsky-Shapirodescribes analyzing and presenting...
) can be used to build higher-dimensional subspaces only by combining lower-dimensional ones, as any subspace T containing a cluster, will result in a full space S also to contain that cluster (i.e. S ⊆ T), an approach taken by most of the traditional algorithms such as CLIQUE and SUBCLU
SUBCLU
SUBCLU is an algorithm for clustering high-dimensional data by Karin Kailing, Hans-Peter Kriegel and Peer Kröger. It is a subspace clustering algorithm that builds on the density-based clustering algorithm DBSCAN...
.
Projected Clustering
Projected clustering seeks to assign each point to a unique cluster, but clusters may exist in different subspaces. The general approach is to use a special distance function together with a regular clustering algorithm.For example, the PreDeCon algorithm checks which attributes seem to support a clustering for each point, and adjusts the distance function such that dimensions with low variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
are amplified in the distance function . In the figure above, the cluster
 might be found using DBSCAN
might be found using DBSCANDBSCAN
DBSCAN is a data clustering algorithm proposed by Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu in 1996....
with a distance function that places less emphasis on the
 -axis and thus exaggerates the low difference in the
-axis and thus exaggerates the low difference in the 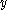 -axis sufficiently enough to group the points into a cluster.
-axis sufficiently enough to group the points into a cluster.PROCLUS uses a similar approach with a k-medoid clustering . Initial medoids are guessed, and for each medoid the subspace spanned by attributes with low variance is determined. Points are assigned to the medoid closest, considering only the subspace of that medoid in determining the distance. The algorithm then proceeds as the regular PAM algorithm.
If the distance function weights attributes differently, but never with 0 (and hence never drops irrelevant attributes), the algorithm is called a "soft"-projected clustering algorithm.
Hybrid Approaches
Not all algorithms try to either find a unique cluster assignment for each point or all clusters in all subspaces; many settle for a result in between, where a number of possibly overlapping, but not necessarily exhaustive set of clusters are found. An example is FIRES, which is from its basic approach a subspace clustering algorithm, but uses a heuristicHeuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
too aggressive to credibly produce all subspace clusters .
Correlation Clustering
Another type of subspaces is considered in Correlation clustering (Data Mining)Correlation clustering
In machine learning, correlation clustering or cluster editing operates in a scenario where the relationship between the objects are known instead of the actual representation of the objects...
.

