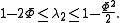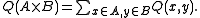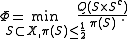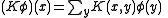Cheeger bound
Encyclopedia
In mathematics
, the Cheeger bound is a bound of the second largest eigenvalue of the transition matrix of a finite-state, discrete-time, reversible stationary Markov chain
. It can be seen as a special case of Cheeger inequalities in expander graphs.
Let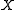 be a finite set and let
be a finite set and let  be the transition probability for a reversible Markov chain on
be the transition probability for a reversible Markov chain on 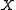 . Assume this chain has stationary distribution
. Assume this chain has stationary distribution
 .
.
Define
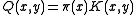
and for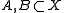 define
define
Define the constant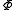 as
as
The operator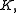 acting on the space of functions from
acting on the space of functions from  to
to 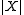 , defined by
, defined by
has eigenvalues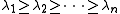 . It is known that
. It is known that 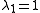 . The Cheeger bound is a bound on the second largest eigenvalue
. The Cheeger bound is a bound on the second largest eigenvalue 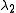 .
.
Theorem (Cheeger bound):
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cheeger bound is a bound of the second largest eigenvalue of the transition matrix of a finite-state, discrete-time, reversible stationary Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
. It can be seen as a special case of Cheeger inequalities in expander graphs.
Let
 be a finite set and let
be a finite set and let  be the transition probability for a reversible Markov chain on
be the transition probability for a reversible Markov chain on 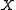 . Assume this chain has stationary distribution
. Assume this chain has stationary distributionStationary distribution
Stationary distribution may refer to:* The limiting distribution in a Markov chain* The marginal distribution of a stationary process or stationary time series* The set of joint probability distributions of a stationary process or stationary time series...
 .
.Define
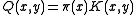
and for
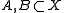 define
defineDefine the constant
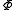 as
asThe operator
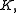 acting on the space of functions from
acting on the space of functions from  to
to 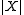 , defined by
, defined byhas eigenvalues
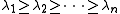 . It is known that
. It is known that 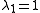 . The Cheeger bound is a bound on the second largest eigenvalue
. The Cheeger bound is a bound on the second largest eigenvalue 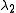 .
.Theorem (Cheeger bound):