Cavalieri's quadrature formula
Encyclopedia
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, Cavalieri's quadrature formula, named for 16th century Italian mathematician Bonaventura Cavalieri
Bonaventura Cavalieri
Bonaventura Francesco Cavalieri was an Italian mathematician. He is known for his work on the problems of optics and motion, work on the precursors of infinitesimal calculus, and the introduction of logarithms to Italy...
, is the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
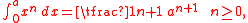
and generalizations thereof. This is the definite integral form; the indefinite integral form is:
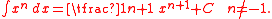
There are additional forms, listed below. Together with the linearity of the integral, this formula allows one to compute the integrals of all polynomials.
The term "quadrature
Quadrature
Quadrature may refer to:In signal processing:*Quadrature amplitude modulation , a modulation method of using both an carrier wave and a 'quadrature' carrier wave that is 90° out of phase with the main, or in-phase, carrier...
" is a traditional term for area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
; the integral is geometrically interpreted as the area under the curve y = xn. Traditionally important cases are y = x2, the quadrature of the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, known in antiquity, and y = 1/x, the quadrature of the hyperbola, whose value is a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
.
Negative n
For negative values of n (negative powers of x), there is a singularityMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
at x = 0, and thus the definite integral is based at 1, rather than 0, yielding:
Further, for negative fractional (non-integer) values of n, the power xn is not well-defined, hence the indefinite integral is only defined for positive x. However for n a negative integer the power xn is defined for all non-zero x, and the indefinite integrals and definite integrals are defined, and can be computed via a symmetry argument, replacing x by −x, and basing the negative definite integral at −1.
Over the complex numbers the definite integral (for negative values of n and x) can be defined via contour integration, but then depends on choice of path, specifically winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
– the geometric issue is that the function defines a covering space with a singularity at 0.
n = −1
There is also the exceptional case n = −1, yielding a logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
instead of a power of x:
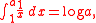
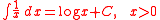
(where "log" means the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, i.e. the logarithm to the base e = 2.71828...).
The improper integral is often extended to negative values of x via the conventional choice:
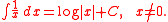
Note the use of the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
in the indefinite integral; this is to provide a unified form for the integral, and means that the integral of this odd function is an even function, though the logarithm is only defined for positive inputs, and in fact, different constant values of C can be chosen on either side of 0, since these do not change the derivative. Over the complex numbers there is not a global antiderivative for 1/x, due this function defining a non-trivial covering space; this form is special to the real numbers.
Note that the definite integral starting from 1 is not defined for negative values of a, since it passes through a singularity, though since 1/x is an odd function, one can base the definite integral for negative powers at −1. If one is willing to use improper integral
Improper integral
In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
s and compute the Cauchy principal value
Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
, one obtains
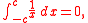which can also be argued by symmetry (since the logarithm is odd), so 
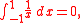so it makes no difference if the definite integral is based at 1 or −1. As with the indefinite integral, this is special to the real numbers, and does not extend over the complex numbers.Alternative forms
The integral can also be written with indexes shifted, which simplify the result and make the relation to n-dimensional differentiation and the n-cube clearer:
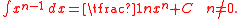
More generally, these formulae may be given as:
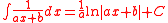
Proof
The modern proof is to use an anti-derivative: the derivative of xn is shown to be nxn−1 – for non-negative integers this is easily shown from the binomial formula and the definition of the derivative – and thus by the fundamental theorem of calculusFundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
the antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
is the integral. This method fails for
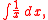as the candidate antiderivative is 
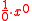, which is undefined due to division by zero. The logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
function, which is the actual antiderivative of 1/x, must be introduced and examined separately.
For positive integers, this proof can be geometrized: if one considers the quantity xn as the volume of the n-cube (the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
in n dimensions), then the derivative is the change in the volume as the side length is changed – this is xn−1, which can be interpreted as the area of n faces, each of dimension n − 1 (fixing one vertex at the origin, these are the n faces not touching the vertex), corresponding to the cube increasing in size by growing in the direction of these faces – in the 3-dimensional case, adding 3 infinitesimally thin squares, one to each of these faces. Conversely, geometrizing the fundamental theorem of calculus, stacking up these infinitesimal (n − 1) cubes yields a (hyper)-pyramid, and n of these pyramids form the n-cube, which yields the formula. Further, there is an n-fold cyclic symmetry of the n-cube around the diagonal cycling these pyramids (for which a pyramid is a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
). In the case of the cube (3-cube), this is how the volume of a pyramid was originally rigorously established: the cube has 3-fold symmetry, with fundamental domain a pyramids, dividing the cube into 3 pyramids, corresponding to the fact that the volume of a pyramid is one third of the base times the height. This illustrates geometrically the equivalence between the quadrature of the parabola and the volume of a pyramid, which were computed classically by different means.
Alternative proofs exist – for example, Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
computed the area via an algebraic trick of dividing the domain into certain intervals of unequal length; alternatively, one can prove this by recognizing a symmetry of the graph y = xn under inhomogeneous dilation (by d in the x direction and dn in the y direction, algebraicizing the n dimensions of the y direction), or deriving the formula for all integer values by expanding the result for n = −1 and comparing coefficients.
History
History of calculus
Calculus, historically known as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Ideas leading up to the notions of function, derivative, and integral were developed throughout the 17th century, but the decisive step was...
and history of integration.
The case of the parabola was proven in antiquity by the ancient Greek mathematician Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in his The Quadrature of the Parabola
The Quadrature of the Parabola
The Quadrature of the Parabola is a treatise on geometry, written by Archimedes in the 3rd century BC. Written as a letter to his friend Dositheus, the work presents 24 propositions regarding parabolas, culminating in a proof that the area of a parabolic segment is 4/3 that of a certain inscribed...
(3rd century BCE), via the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
. Of note is that Archimedes computed the area inside a parabola – a so-called "parabolic segment" – rather than the area under the graph y = x2, which is instead the perspective of Cartesian geometry. These are equivalent computations, but reflect a difference in perspective. The Ancient Greeks, among others, also computed the volume of a pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
or cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
, which is mathematically equivalent.
In the 11th century, the Islamic mathematician
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
Ibn al-Haytham (known as Alhazen in Europe) computed the integrals of cubics and quartics (degree three and four) via mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, in his Book of Optics
Book of Optics
The Book of Optics ; ; Latin: De Aspectibus or Opticae Thesaurus: Alhazeni Arabis; Italian: Deli Aspecti) is a seven-volume treatise on optics and other fields of study composed by the medieval Muslim scholar Alhazen .-See also:* Science in medieval Islam...
.
The case of higher integers was computed by Cavalieri for n up to 9, using his method of indivisibles (Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
). He interpreted these as higher integrals as computing higher dimensional volumes, though only informally, as higher dimensional objects were as yet unfamiliar. This method of quadrature was then extended by Italian mathematician Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
to other curves such as the cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, then the formula was generalized to fractional and negative powers by English mathematician John Wallis, in his Arithmetica Infinitorum (1656), which also standardized the notion and notation of rational powers – though Wallis incorrect interpreted the exceptional case n = −1 (quadrature of the hyperbola) – before finally being put on rigorous ground with the development of integral calculus.
Prior to Wallis's formalization of fractional and negative powers, which allowed explicit functions
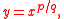these curves were handled implicitly, via the equations 
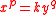and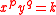 
(p and q always positive integers) and referred to respectively as higher parabolae and higher hyperbolae (or "higher parabolas" and "higher hyperbolas"). Pierre de FermatPierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
also computed these areas (except for the exceptional case of −1) by an algebraic trick – he computed the quadrature of the higher hyperbolae via dividing the line into equal intervals, and then computed the quadrature of the higher parabolae by using a division into unequal intervals, presumably by inverting the divisions he used for hyperbolae. However, as in the rest of his work, Fermat's techniques were more ad hoc tricks than systematic treatments, and he is not considered to have played a significant part in the subsequent development of calculus.
Of note is that Cavalieri only compared areas to areas and volumes to volumes – these always having dimensions, while the notion of considering an area as consisting of units of area (relative to a standard unit), hence being unitless, appears to have originated with Wallis; Wallis studied fractional and negative powers, and the alternative to treating the computed values as unitless numbers was to interpret fractional and negative dimensions.
The exceptional case of −1 (the standard hyperbola) was first successfully treated by Grégoire de Saint-Vincent
Grégoire de Saint-Vincent
Grégoire de Saint-Vincent , a Jesuit, was a mathematician who discovered that the area under a rectangular hyperbola is the same over [a,b] as over [c,d] when a/b = c/d...
in his Opus geometricum quadrature circuli et sectionum coni (1647), though a formal treatment had to wait for the development of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, which was accomplished by Nicholas Mercator
Nicholas Mercator
Nicholas Mercator , also known by his Germanic name Kauffmann, was a 17th-century mathematician....
in his Logarithmotechnia (1668).
History
- Cavalieri, Geometria indivisibilibus (continuorum nova quadam ratione promota) (Geometry, exposed in a new manner with the aid of indivisibles of the continuous), 1635.
- Cavalieri, Exercitationes Geometricae Sex ("Six Geometrical Exercises"), 1647
- in Dirk Jan StruikDirk Jan StruikDirk Jan Struik was a Dutch mathematician and Marxian theoretician who spent most of his life in the United States.- Life :...
, editor, A source book in mathematics, 1200–1800 (Princeton University Press, Princeton, New Jersey, 1986). ISBN 0-691-08404-1, ISBN 0-691-02397-2 (pbk).
- in Dirk Jan Struik
- Mathematical expeditions: chronicles by the explorers, Reinhard Laubenbacher, David Pengelley, 1998, Section 3.4: "Cavalieri Calculates Areas of Higher Parabolas", pp. 123–127/128
- A short account of the history of mathematics, Walter William Rouse Ball, "Cavalieri", p. 278–281
- "Infinitesimal calculus", Encyclopaedia of Mathematics
- The Britannica Guide to Analysis and Calculus, by Educational Britannica Educational, p. 171 – discusses Wallace primarily
Proofs
- "Fermat's Integration of Powers", in Historical Notes for Calculus Teachers by V. Frederick Rickey – gives Fermat's algebraic proof of the formula in modern language
- A geometric proof of Cavalieri's quadrature formula, Ilan Vardi