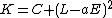Carter constant
Encyclopedia
The Carter constant is a conserved quantity
for motion around black hole
s in the general relativistic
formulation of gravity. Carter's constant was derived for a spinning, charged black hole by Australian theoretical physicist Brandon Carter
in 1968. Carter's constant along with the energy, axial angular momentum, and particle rest mass provide the four conserved quantities necessary to uniquely determine all orbits in the Kerr-Newman
spacetime (even those of charged particles).
, allowing the constants of such motion to be easily identified using Hamilton-Jacobi theory
. The Carter constant can be written as follows:
where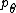
is the latitudinal component of the particle's momentum, 
is the energy of the particle, 
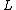is the particle's axial angular momentum, 
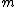is the rest mass of the particle, and 
is the spin parameter of the black hole. Because functions of conserved quantities are also conserved, any function of 
and the three other constants of the motion can be used as a fourth constant in place of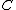 
. This results in some confusion as to the form of Carter's constant. For example it is sometimes more convenient to use:
in place of
. The quantity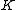 
is useful because it is always non-negative. In general any fourth conserved quantity for motion in the Kerr
family of spacetimes may be referred to as "Carter's constant".
states that all conserved quantities are related to spacetime symmetries
. Carter's constant is related to a higher order symmetry of the Kerr metric generated by a second order Killing tensor field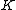
(different 
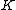than used above). In component form:
where
is the four-velocity
of the particle in motion. The components of the Killing tensor in Boyer-Lindquist coordinates
are:
where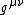
are the components of the metric tensor and 
and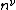 
are the components of the principal null vectors:
.
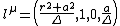
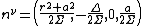for non-spinning black holes allows one to reduce the problem of finding the trajectories of particles to three dimensions. In this case one only needs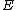
, 
, and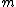 
to determine the motion; however, the symmetry leading to Carter's constant still exists. Carter's constant for Schwarzschild space is:
By a rotation of coordinates we can put any orbit in the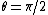
plane so 
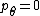. In this case 
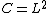, the square of the orbital angular momentum.
Conserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
for motion around black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s in the general relativistic
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
formulation of gravity. Carter's constant was derived for a spinning, charged black hole by Australian theoretical physicist Brandon Carter
Brandon Carter
Brandon Carter, FRS is an Australian theoretical physicist, best known for his work on the properties of black holes and for being the first to name and employ the anthropic principle in its contemporary form. He is a researcher at the Meudon campus of the Laboratoire Univers et Théories, part of...
in 1968. Carter's constant along with the energy, axial angular momentum, and particle rest mass provide the four conserved quantities necessary to uniquely determine all orbits in the Kerr-Newman
Kerr-Newman metric
The Kerr–Newman metric is a solution of the Einstein–Maxwell equations in general relativity, describing the spacetime geometry in the region surrounding a charged, rotating mass. It is assumed that the cosmological constant equals zero...
spacetime (even those of charged particles).
Formulation
Carter noticed that the Hamiltonian for motion in Kerr spacetime was separable in Boyer-Lindquist coordinatesBoyer-Lindquist coordinates
A generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.The coordinate transformation from Boyer–Lindquist coordinates r, \theta, \phi to cartesian coordinates x, y, z is given bywhereThe Hamiltonian for test...
, allowing the constants of such motion to be easily identified using Hamilton-Jacobi theory
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
. The Carter constant can be written as follows:
-
,
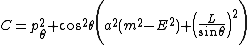where
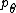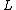is the latitudinal component of the particle's momentum, is the energy of the particle, is the particle's axial angular momentum, 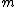is the rest mass of the particle, and is the spin parameter of the black hole. Because functions of conserved quantities are also conserved, any function of and the three other constants of the motion can be used as a fourth constant in place of 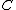. This results in some confusion as to the form of Carter's constant. For example it is sometimes more convenient to use:
in place of
. The quantity 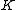is useful because it is always non-negative. In general any fourth conserved quantity for motion in the KerrKerr metric
The Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
family of spacetimes may be referred to as "Carter's constant".
As generated by a Killing tensor
Noether's theoremNoether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
states that all conserved quantities are related to spacetime symmetries
Spacetime symmetries
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...
. Carter's constant is related to a higher order symmetry of the Kerr metric generated by a second order Killing tensor field
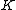(different 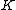than used above). In component form:-
,
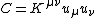where
is the four-velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
of the particle in motion. The components of the Killing tensor in Boyer-Lindquist coordinates
Boyer-Lindquist coordinates
A generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.The coordinate transformation from Boyer–Lindquist coordinates r, \theta, \phi to cartesian coordinates x, y, z is given bywhereThe Hamiltonian for test...
are:
-
,
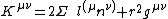where
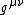are the components of the metric tensor and and 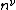are the components of the principal null vectors: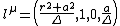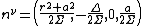.Schwarzschild limit
The spherical symmetry of the Schwarzschild metricSchwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
for non-spinning black holes allows one to reduce the problem of finding the trajectories of particles to three dimensions. In this case one only needs
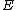, , and 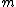to determine the motion; however, the symmetry leading to Carter's constant still exists. Carter's constant for Schwarzschild space is:-
.
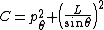By a rotation of coordinates we can put any orbit in the
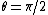plane so 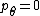. In this case 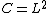, the square of the orbital angular momentum.See also
- Kerr metricKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
- Kerr-Newman metricKerr-Newman metricThe Kerr–Newman metric is a solution of the Einstein–Maxwell equations in general relativity, describing the spacetime geometry in the region surrounding a charged, rotating mass. It is assumed that the cosmological constant equals zero...
- Boyer-Lindquist coordinatesBoyer-Lindquist coordinatesA generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.The coordinate transformation from Boyer–Lindquist coordinates r, \theta, \phi to cartesian coordinates x, y, z is given bywhereThe Hamiltonian for test...
- Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...