
CGHS model
Encyclopedia
The Callan-Giddings-Harvey-Strominger model or CGHS in short is a toy model
of general relativity
in 1 spatial and 1 time dimension. General relativity is a highly nonlinear model, and as such, its 3+1D version is usually too complicated to analyze in detail. In 3+1D and higher, propagating gravitational wave
s exist, but not in 2+1D or 1+1D. In 2+1D, general relativity becomes a topological field theory with no local degrees of freedom, and all 1+1D models are locally flat
. However, a slightly more complicated generalization of general relativity which includes dilaton
s will turn the 2+1D model into one admitting mixed propagating dilaton-gravity waves, as well as making the 1+1D model geometrically nontrivial locally. The 1+1D model still does not admit any propagating gravitational (or dilaton) degrees of freedom, but with the addition of matter fields, it becomes a simplified, but still nontrivial model. With other numbers of dimensions, a dilaton-gravity coupling can always be rescaled away by a conformal rescaling of the metric, converting the Jordan frame to the Einstein frame. But not in two dimensions, because the conformal weight of the dilaton is now 0. The metric in this case is more amenable to analytical solutions than the general 3+1D case. And of course, 0+1D models cannot capture any nontrivial aspect of relativity because there is no space at all.
This class of models retains just enough complexity to include among its solutions black hole
s, their formation, FRW cosmological models, gravitational singularities, etc. In the quantized version of such models with matter fields, Hawking radiation
also shows up, just as in higher dimensional models.
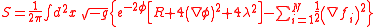
where g is the metric tensor
, φ is the dilaton field, fi are the matter fields, and λ2 is the cosmological constant
. In particular, the cosmological constant is nonzero, and the matter fields are massless real scalars.
This specific choice is classically integrable, but still not amenable to an exact quantum solution. It is also the action for Non-critical string theory
and dimensional reduction
of higher dimensional model. It also distinguishes it from Jackiw–Teitelboim gravity and Liouville gravity, which are entirely different models.
The matter field only couples to the causal structure
, and in the light-cone gauge , has the simple generic form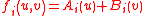 ,
,
with a factorization between left- and right-movers.
The Raychaudhuri equations are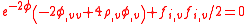 and
and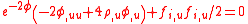 .
.
The dilaton evolves according to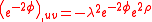 ,
,
while the metric evolves according to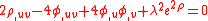 .
.
The conformal anomaly
due to matter induces a Liouville term in the effective action
.
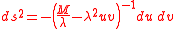
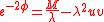 ,
,
where M is the ADM mass.
Singularities appear at .
The masslessness of the matter fields allow a black hole to completely evaporate away via Hawking radiation
. In fact, this model was originally studied to shed light upon the black hole information paradox
.
Toy model
In physics, a toy model is a simplified set of objects and equations relating them that can nevertheless be used to understand a mechanism that is also useful in the full, non-simplified theory....
of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
in 1 spatial and 1 time dimension. General relativity is a highly nonlinear model, and as such, its 3+1D version is usually too complicated to analyze in detail. In 3+1D and higher, propagating gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
s exist, but not in 2+1D or 1+1D. In 2+1D, general relativity becomes a topological field theory with no local degrees of freedom, and all 1+1D models are locally flat
Flat
In music, flat, or Bemolle , means "lower in pitch"; the flat symbol lowers a note by a half step. Intonation may be flat, sharp, or both, successively or simultaneously...
. However, a slightly more complicated generalization of general relativity which includes dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
s will turn the 2+1D model into one admitting mixed propagating dilaton-gravity waves, as well as making the 1+1D model geometrically nontrivial locally. The 1+1D model still does not admit any propagating gravitational (or dilaton) degrees of freedom, but with the addition of matter fields, it becomes a simplified, but still nontrivial model. With other numbers of dimensions, a dilaton-gravity coupling can always be rescaled away by a conformal rescaling of the metric, converting the Jordan frame to the Einstein frame. But not in two dimensions, because the conformal weight of the dilaton is now 0. The metric in this case is more amenable to analytical solutions than the general 3+1D case. And of course, 0+1D models cannot capture any nontrivial aspect of relativity because there is no space at all.
This class of models retains just enough complexity to include among its solutions black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s, their formation, FRW cosmological models, gravitational singularities, etc. In the quantized version of such models with matter fields, Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
also shows up, just as in higher dimensional models.
Action
A very specific choice of couplings and interactions leads to the CGHS model.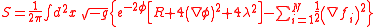
where g is the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, φ is the dilaton field, fi are the matter fields, and λ2 is the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
. In particular, the cosmological constant is nonzero, and the matter fields are massless real scalars.
This specific choice is classically integrable, but still not amenable to an exact quantum solution. It is also the action for Non-critical string theory
Non-critical string theory
The non-critical string theory describes the relativistic string without enforcing the critical dimension. Although this allows the construction of a string theory in 4 spacetime dimensions, such a theory usually does not describe a Lorentz invariant background. However, there are recent...
and dimensional reduction
Dimensional reduction
In physics, a theory in D spacetime dimensions can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions....
of higher dimensional model. It also distinguishes it from Jackiw–Teitelboim gravity and Liouville gravity, which are entirely different models.
The matter field only couples to the causal structure
Causal structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
, and in the light-cone gauge , has the simple generic form
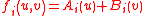 ,
,with a factorization between left- and right-movers.
The Raychaudhuri equations are
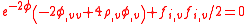 and
and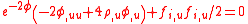 .
.The dilaton evolves according to
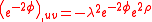 ,
,while the metric evolves according to
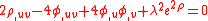 .
.The conformal anomaly
Conformal anomaly
Conformal anomaly is an anomaly i.e. a quantum phenomenon that breaks the conformal symmetry of the classical theory.A classically conformal theory is a theory which, when placed on a surface with arbitrary background metric, has an action that is invariant under rescalings of the background metric...
due to matter induces a Liouville term in the effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
.
Black hole
A vacuum black hole solution is given by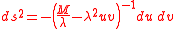
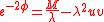 ,
,where M is the ADM mass.
Singularities appear at .
The masslessness of the matter fields allow a black hole to completely evaporate away via Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
. In fact, this model was originally studied to shed light upon the black hole information paradox
Black hole information paradox
The black hole information paradox results from the combination of quantum mechanics and general relativity. It suggests that physical information could disappear in a black hole, allowing many physical states to evolve into the same state...
.
See also
- dilatonDilatonIn particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
- general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
- quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
- RST modelRST modelThe Russo-Susskind-Thorlacius model or RST model in short is a modification of the CGHS model to take care of conformal anomalies. In the CGHS model, if we include Faddeev-Popov ghosts to gauge-fix diffeomorphisms in the conformal gauge, they contribute an anomaly of -24. Each matter field...
- Jackiw–Teitelboim gravity
- Liouville gravity

