Bézout's theorem
Encyclopedia
Bézout's theorem is a statement in algebraic geometry
concerning the number of common points, or intersection points, of two plane algebraic curve
s. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degree
s. This statement must be qualified in several important ways, by considering points at infinity, allowing complex coordinates (or more generally, coordinates from the algebraic closure
of the ground field), assigning an appropriate multiplicity
to each intersection point, and excluding a degenerate case when X and Y have a common component. A simpler special case is that if X and
Y are both real or complex irreducible curve
s, X has degree m and Y has degree n then the number of intersection points does not exceed mn.
More generally, number of points in the intersection of 3 algebraic surfaces in projective space is, counting multiplicities, the product of the degrees of the equations of the surfaces, and so on.
curves defined over a field
F that do not have a common component (this condition is true if both X and Y are defined by different irreducible polynomials, in particular, it holds for a pair of "generic" curves). Then the total number of intersection points of X and Y with coordinates in an algebraically closed field
E which contains F, counted with their multiplicities
, is equal to the product of the degrees of X and Y.
of volume 1 of his principia, where he claims that two curves have a number of intersection points given by the product of their degrees. The theorem was later published in 1779 in Étienne Bézout
's Théorie générale des équations algébriques. Bézout, who did not have at his disposal modern algebraic notation for equations in several variables, gave a proof based on manipulations with cumbersome algebraic expressions. From the modern point of view, Bézout's treatment was rather heuristic, since he did not formulate the precise conditions for the theorem to hold. This led to a sentiment, expressed by certain authors, that his proof was neither correct nor the first proof to be given.
is the procedure of assigning the proper intersection multiplicities. If P is a common point of two plane algebraic curves X and Y that is a non-singular point of both of them and, moreover, the tangent lines to X and Y at P are distinct then the intersection multiplicity is one. This corresponds to the case of "transversal intersection". If the curves X and Y have a common tangent at P then the multiplicity is at least two. See intersection number
for the definition in general.
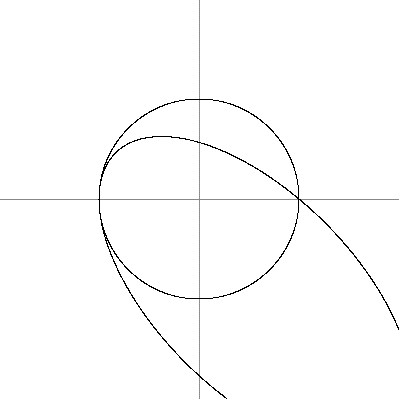

as

where ai and bi are homogeneous polynomials of degree i in x and y. The points of intersection of X and Y correspond to the solutions of the system of equations. Form the Sylvester matrix
; in the case m=4, n=3 this is

The determinant
of S, the resultant of the two polynomials, is 0 exactly when the two equations have a common solution in z. The terms of |S|, for example (a0)n(bn)m, all have degree mn, so |S| is a homogeneous polynomial of degree mn in x and y (recall that ai and bi are themselves polynomials). By the fundamental theorem of algebra
, this can be factored into mn linear factors so there are mn solutions to the system of equations. The linear factors correspond to the lines that join the origin to the points of intersection of the curves.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
concerning the number of common points, or intersection points, of two plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
s. This statement must be qualified in several important ways, by considering points at infinity, allowing complex coordinates (or more generally, coordinates from the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the ground field), assigning an appropriate multiplicity
Intersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
to each intersection point, and excluding a degenerate case when X and Y have a common component. A simpler special case is that if X and
Y are both real or complex irreducible curve
Irreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
s, X has degree m and Y has degree n then the number of intersection points does not exceed mn.
More generally, number of points in the intersection of 3 algebraic surfaces in projective space is, counting multiplicities, the product of the degrees of the equations of the surfaces, and so on.
Rigorous statement
Suppose that X and Y are two plane projectiveProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
curves defined over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F that do not have a common component (this condition is true if both X and Y are defined by different irreducible polynomials, in particular, it holds for a pair of "generic" curves). Then the total number of intersection points of X and Y with coordinates in an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
E which contains F, counted with their multiplicities
Intersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
, is equal to the product of the degrees of X and Y.
History
Bezout's theorem was essentially stated by Isaac Newton in his proof of lemma 28Newton's theorem about ovals
In mathematics, Newton's theorem about ovals states that the area cut off by a secant of a smooth convex oval is not an algebraic function of the secant....
of volume 1 of his principia, where he claims that two curves have a number of intersection points given by the product of their degrees. The theorem was later published in 1779 in Étienne Bézout
Étienne Bézout
-External links:...
's Théorie générale des équations algébriques. Bézout, who did not have at his disposal modern algebraic notation for equations in several variables, gave a proof based on manipulations with cumbersome algebraic expressions. From the modern point of view, Bézout's treatment was rather heuristic, since he did not formulate the precise conditions for the theorem to hold. This led to a sentiment, expressed by certain authors, that his proof was neither correct nor the first proof to be given.
Intersection multiplicity
The most delicate part of Bézout's theorem and its generalization to the case of k algebraic hypersurfaces in k-dimensional projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
is the procedure of assigning the proper intersection multiplicities. If P is a common point of two plane algebraic curves X and Y that is a non-singular point of both of them and, moreover, the tangent lines to X and Y at P are distinct then the intersection multiplicity is one. This corresponds to the case of "transversal intersection". If the curves X and Y have a common tangent at P then the multiplicity is at least two. See intersection number
Intersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
for the definition in general.
Examples
- Two distinct non-parallel lines always meet in exactly one point. Two parallel lines intersect at a unique point that lies at infinity. To see how this works algebraically, in projective space, the lines x+2y=3 and x+2y=5 are represented by the homogeneous equations x+2y-3z=0 and x+2y-5z=0. Solving, we get x= -2y and z=0, corresponding to the point (-2:1:0) in homogeneous coordinates. As the z-coordinate is 0, this point lies on the line at infinity.
- The special case where one of the curves is a line can be derived from the fundamental theorem of algebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
. In this case the theorem states that an algebraic curve of degree n intersects a given line in n points, counting the multiplicities. For example, the parabola defined by y - x2 = 0 has degree 2; the line y − ax = 0 has degree 1, and they meet in exactly two points when a ≠ 0 and touch at the origin (intersect with multiplicity two) when a = 0.
- Two conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s generally intersect in four points, some of which may coincide. To properly account for all intersection points, it may be necessary to allow complex coordinates and include the points on the infinite line in the projective plane. For example:
- Two circles never intersect in more than two points in the plane, while Bézout's theorem predicts four. The discrepancy comes from the fact that every circle passes through the same two complex points on the line at infinity. Writing the circle
-
- in homogeneous coordinatesHomogeneous coordinatesIn mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, we get - from which it is clear that the two points (1:i:0) and (1:-i:0) lie on every circle. When two circles don't meet at all in the real plane (for example because they are concentric) they meet at these two points on the line at infinity and two other complex points which do not lie at infinity.
- Any conic should meet the line at infinity at two points according to the theorem. A hyperbola meets it at two real points corresponding to the two directions of the asymptotes. An ellipse meets it at two complex points which are conjugate to one another---in the case of a circle, the points (1:i:0) and (1:-i:0). A parabola meets it at only one point, but it is a point of tangency and therefore counts twice.
- The following pictures show examples in which the circle x2+y2-1=0 meets another ellipse in fewer intersection points because at least one of them has multiplicity greater than 1:

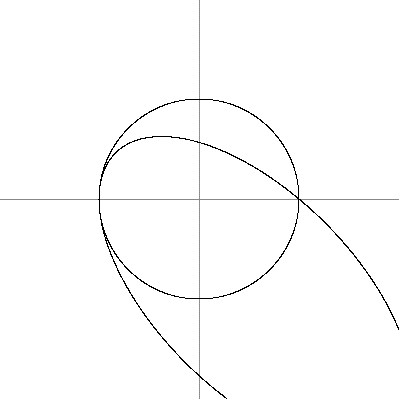

Informal proof
Write the equations for X and Y in homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
as


where ai and bi are homogeneous polynomials of degree i in x and y. The points of intersection of X and Y correspond to the solutions of the system of equations. Form the Sylvester matrix
Sylvester matrix
In mathematics, a Sylvester matrix is a matrix associated to two polynomials that provides information about those polynomials. It is named for James Joseph Sylvester.-Definition:...
; in the case m=4, n=3 this is

The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of S, the resultant of the two polynomials, is 0 exactly when the two equations have a common solution in z. The terms of |S|, for example (a0)n(bn)m, all have degree mn, so |S| is a homogeneous polynomial of degree mn in x and y (recall that ai and bi are themselves polynomials). By the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
, this can be factored into mn linear factors so there are mn solutions to the system of equations. The linear factors correspond to the lines that join the origin to the points of intersection of the curves.






