Bézout's identity
Encyclopedia
In number theory
, Bézout's identity for two integers a, b is an expression
where x and y are integers (called Bézout coefficients for (a,b)), such that d is a common divisor
of a and b. Bézout's lemma
states that such coefficients exist for every pair of nonzero integers (a,b). In addition is their greatest common divisor
and the smallest positive integer that can be written, in this form, for any integers x,y. This value of d is therefore uniquely determined by a and b, but the Bézout coefficients are not unique. A pair of Bézout coefficients (in fact the ones that are minimal in absolute value
) can be computed by the extended Euclidean algorithm
. The identity, coefficients and lemma are named after the French
mathematician
Étienne Bézout
.
In abstract algebra
, certain pairs of elements of an integral domain may also admit such an identity, but this need not be the case for all pairs of nonzero elements. Bézout's lemma does however remain valid in any principal ideal domain
.
(1730–1783) proved this identity for polynomials. However, this statement for integers can be found already in the work of French mathematician Claude Gaspard Bachet de Méziriac
(1581–1638).
. However, they are not unique. If one solution is given by (x, y), then there are infinitely many solutions. These are given by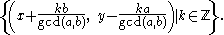
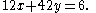
One of its solutions is x = −3 and y = 1: indeed, we have (−3)·12 + 1·42 = 6. Another solution is x = 4 and y = −1.
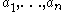with greatest common divisor d there exist integers 
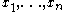such that
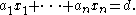
The greatest common divisor of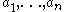
is in fact the smallest positive integer that can be written as a linear combination of 
.
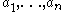Bézout's identity works not only in the ring of integers, but also in any other principal ideal domain
(PID).
That is, if R is a PID, and a and b are elements of R, and d is a greatest common divisor of a and b,
then there are elements x and y in R such that ax + by = d. The reason: the ideal
Ra+Rb is principal and indeed is equal to Rd.
An integral domain in which Bézout's identity holds is called a Bézout domain
.
(for the absolute value), as affirmed by the defining property of Euclidean division of integers, namely that the remainder of a division by a nonzero integer b has a remainder
strictly less than |b|. For given nonzero integers a and b there is a nonzero integer of minimal absolute among all those of the form ax + by with x and y integers; one can assume d > 0 by changing the signs of both s and t if necessary. Now the remainder of dividing either a or b by d is also of the form ax + by since it is obtained by subtracting a multiple of from a or b, and on the other hand it has to be strictly smaller in absolute value than d. This leaves 0 as only possibility for such a remainder, so d divides a and b exactly.
If c is another common divisor of a and b, then c also divides as + bt = d, which means that d is the greatest common divisor of a and b; this completes the proof.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Bézout's identity for two integers a, b is an expression
where x and y are integers (called Bézout coefficients for (a,b)), such that d is a common divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of a and b. Bézout's lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
states that such coefficients exist for every pair of nonzero integers (a,b). In addition is their greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
and the smallest positive integer that can be written, in this form, for any integers x,y. This value of d is therefore uniquely determined by a and b, but the Bézout coefficients are not unique. A pair of Bézout coefficients (in fact the ones that are minimal in absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
) can be computed by the extended Euclidean algorithm
Extended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
. The identity, coefficients and lemma are named after the French
French people
The French are a nation that share a common French culture and speak the French language as a mother tongue. Historically, the French population are descended from peoples of Celtic, Latin and Germanic origin, and are today a mixture of several ethnic groups...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Étienne Bézout
Étienne Bézout
-External links:...
.
In abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, certain pairs of elements of an integral domain may also admit such an identity, but this need not be the case for all pairs of nonzero elements. Bézout's lemma does however remain valid in any principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
.
History
Étienne BézoutÉtienne Bézout
-External links:...
(1730–1783) proved this identity for polynomials. However, this statement for integers can be found already in the work of French mathematician Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...
(1581–1638).
Algorithm
The Bézout numbers x and y as above can be determined with the extended Euclidean algorithmExtended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
. However, they are not unique. If one solution is given by (x, y), then there are infinitely many solutions. These are given by
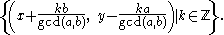
Example
The greatest common divisor of 12 and 42 is 6. Bézout's identity states that there must exist an integer solution for x and y in the following equation: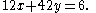One of its solutions is x = −3 and y = 1: indeed, we have (−3)·12 + 1·42 = 6. Another solution is x = 4 and y = −1.
Generalizations
Bézout's identity can be extended to linear combinations of more than two numbers. For any numbers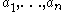 with greatest common divisor d there exist integers 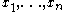such that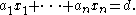The greatest common divisor of
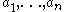is in fact the smallest positive integer that can be written as a linear combination of 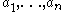.Bézout's identity works not only in the ring of integers, but also in any other principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(PID).
That is, if R is a PID, and a and b are elements of R, and d is a greatest common divisor of a and b,
then there are elements x and y in R such that ax + by = d. The reason: the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
Ra+Rb is principal and indeed is equal to Rd.
An integral domain in which Bézout's identity holds is called a Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
.
Proof
A proof of Bézout's lemma can be given using of the fact that the integers form a Euclidean domainEuclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
(for the absolute value), as affirmed by the defining property of Euclidean division of integers, namely that the remainder of a division by a nonzero integer b has a remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
strictly less than |b|. For given nonzero integers a and b there is a nonzero integer of minimal absolute among all those of the form ax + by with x and y integers; one can assume d > 0 by changing the signs of both s and t if necessary. Now the remainder of dividing either a or b by d is also of the form ax + by since it is obtained by subtracting a multiple of from a or b, and on the other hand it has to be strictly smaller in absolute value than d. This leaves 0 as only possibility for such a remainder, so d divides a and b exactly.
If c is another common divisor of a and b, then c also divides as + bt = d, which means that d is the greatest common divisor of a and b; this completes the proof.
See also
- AF+BG theoremAF+BG theoremIn algebraic geometry, a field of mathematics, the AF+BG theorem is a result of Max Noether which describes when the equation of an algebraic curve in the complex projective plane can be written in terms of the equations of two other algebraic curves....
, an analogue of Bézout's identity for polynomials - Fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
External links
- Online calculator of Bézout's identity.