Buffon's needle
Encyclopedia
In mathematics
, Buffon's needle problem is a question first posed in the 18th century by Georges-Louis Leclerc, Comte de Buffon
:
Buffon's needle was the earliest problem in geometric probability
to be solved; it can be solved using integral geometry
. The solution, in the case where the needle length is not greater than the width of the strips, can be used to design a Monte Carlo method
for approximating the number π
.
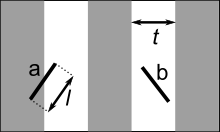The problem in more mathematical terms is: Given a needle of length 
dropped on a plane ruled with parallel lines t units apart, what is the probability that the needle will cross a line?
Let x be the distance from the center of the needle to the closest line, let θ be the acute angle between the needle and the lines.
The uniform probability density function
of x between 0 and t /2 is
The uniform probability density function of θ between 0 and π/2 is
The two random variables, x and θ, are independent, so the joint probability density function is the product
The needle crosses a line if
Now there are two cases.
.
Integrating the joint probability density function gives the probability that the needle will cross a line:
. In this case, integrating the joint probability density function, we obtain:
where
is the minimum between
and 
.
Thus, performing the above integration, we see that,
when
,
the probability that the needle will cross a line is
or
In the second expression, the first term represents the probability of the angle of the needle being such that it will always cross at least one line. The right term represents the probability that, the needle falls at an angle where its position matters, and it crosses the line.
We can calculate the probability
as the product of 2 probabilities: 
, where 
is the probability that the center of the needle falls close enough to a line for the needle to possibly cross it, and 
is the probability that the needle actually crosses the line, given that the center is within reach.
Looking at the illustration in the above section, it is apparent that the needle can cross a line if the center of the needle is within
units of either side of the strip. Adding 
from both sides and dividing by the whole width 
, we obtain 
.
Now, we assume that the center is within reach of the edge of the strip, and calculate
. To simplify the calculation, we can assume that 
.
Let x and θ be as in the illustration in this section. Placing a needle's center at x, the needle will cross the vertical axis if it falls within a range of 2θ radians, out of π radians of possible orientations. This is the gray area in the figure. For a fixed x, we can express θ as a function of x:
. Now we can let x move from 0 to 1, and integrate:
.
Multiplying both results, we obtain
, as above.
Estimating
In the first, simpler case above, the formula obtained for the probability 
can be rearranged to: 
. Thus, if we conduct an experiment to estimate 
, we will also have an estimate for π.
Suppose we drop n needles and find that h of those needles are crossing lines, so
is approximated by the fraction 
. This leads to the formula:
In 1901, Italian
mathematician Mario Lazzarini, performed the Buffon's needle experiment. Tossing a needle 3408 times, he obtained the well-known estimate 355/113 for π, which is a very accurate value, differing from π by no more than 3×10−7. This is an impressive result, but is something of a cheat, as follows.
Lazzarini chose needles whose length was 5/6 of the width of the strips of wood. In this case, the probability that the needles will cross the lines is 5/3π. Thus if one were to drop n needles and get x crossings, one would estimate π as
π is very nearly 355/113; in fact, there is no better rational approximation with fewer than 5 digits in the numerator and denominator. So if one had n and x such that:
or equivalently,
one would derive an unexpectedly accurate approximation to π, simply because the fraction 355/113 happens to be so close to the correct value. But this is easily arranged. To do this, one should pick n as a multiple of 213, because then 113n/213 is an integer; one then drops n needles, and hopes for exactly x = 113n/213 successes.
If one drops 213 needles and happens to get 113 successes, then one can triumphantly report an estimate of π accurate to six decimal places. If not, one can just do 213 more trials and hope for a total of 226 successes; if not, just repeat as necessary. Lazzarini performed 3408 = 213 · 16 trials, making it seem likely that this is the strategy he used to obtain his "estimate".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Buffon's needle problem is a question first posed in the 18th century by Georges-Louis Leclerc, Comte de Buffon
Georges-Louis Leclerc, Comte de Buffon
Georges-Louis Leclerc, Comte de Buffon was a French naturalist, mathematician, cosmologist, and encyclopedic author.His works influenced the next two generations of naturalists, including Jean-Baptiste Lamarck and Georges Cuvier...
:
- Suppose we have a floorFloorA floor is the walking surface of a room or vehicle. Floors vary from simple dirt in a cave to many-layered surfaces using modern technology...
made of parallelParallel (geometry)Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
strips of woodWoodWood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression...
, each the same width, and we drop a needleSewing needleA sewing needle is a long slender tool with a pointed tip. The first needles were made of bone or wood; modern ones are manufactured from high carbon steel wire, nickel- or 18K gold plated for corrosion resistance. The highest quality embroidery needles are plated with two-thirds platinum and...
onto the floor. What is the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the needle will lie across a line between two strips?
Buffon's needle was the earliest problem in geometric probability
Geometric probability
Problems of the following type, and their solution techniques, were firststudied in the 19th century, and the general topic became known as geometric probability....
to be solved; it can be solved using integral geometry
Integral geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...
. The solution, in the case where the needle length is not greater than the width of the strips, can be used to design a Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
for approximating the number π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
Solution
dropped on a plane ruled with parallel lines t units apart, what is the probability that the needle will cross a line?Let x be the distance from the center of the needle to the closest line, let θ be the acute angle between the needle and the lines.
The uniform probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of x between 0 and t /2 is
The uniform probability density function of θ between 0 and π/2 is
The two random variables, x and θ, are independent, so the joint probability density function is the product
The needle crosses a line if
Now there are two cases.
Case 1: Short needle
Suppose.Integrating the joint probability density function gives the probability that the needle will cross a line:
Case 2: Long needle
Suppose. In this case, integrating the joint probability density function, we obtain:where
is the minimum between and .Thus, performing the above integration, we see that,
when
,the probability that the needle will cross a line is
or
In the second expression, the first term represents the probability of the angle of the needle being such that it will always cross at least one line. The right term represents the probability that, the needle falls at an angle where its position matters, and it crosses the line.
Using elementary calculus
The following solution for the "short needle" case, while equivalent to the one above, has a more visual flavor, and avoids iterated integrals.We can calculate the probability
as the product of 2 probabilities: , where is the probability that the center of the needle falls close enough to a line for the needle to possibly cross it, and is the probability that the needle actually crosses the line, given that the center is within reach.Looking at the illustration in the above section, it is apparent that the needle can cross a line if the center of the needle is within
units of either side of the strip. Adding from both sides and dividing by the whole width , we obtain .Now, we assume that the center is within reach of the edge of the strip, and calculate
. To simplify the calculation, we can assume that .Let x and θ be as in the illustration in this section. Placing a needle's center at x, the needle will cross the vertical axis if it falls within a range of 2θ radians, out of π radians of possible orientations. This is the gray area in the figure. For a fixed x, we can express θ as a function of x:
. Now we can let x move from 0 to 1, and integrate:.Multiplying both results, we obtain
, as above. Estimating 
In the first, simpler case above, the formula obtained for the probability can be rearranged to: . Thus, if we conduct an experiment to estimate , we will also have an estimate for π.Suppose we drop n needles and find that h of those needles are crossing lines, so
is approximated by the fraction . This leads to the formula:In 1901, Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
mathematician Mario Lazzarini, performed the Buffon's needle experiment. Tossing a needle 3408 times, he obtained the well-known estimate 355/113 for π, which is a very accurate value, differing from π by no more than 3×10−7. This is an impressive result, but is something of a cheat, as follows.
Lazzarini chose needles whose length was 5/6 of the width of the strips of wood. In this case, the probability that the needles will cross the lines is 5/3π. Thus if one were to drop n needles and get x crossings, one would estimate π as
- π ≈ 5/3 · n/x
π is very nearly 355/113; in fact, there is no better rational approximation with fewer than 5 digits in the numerator and denominator. So if one had n and x such that:
- 355/113 = 5/3 · n/x
or equivalently,
- x = 113n/213
one would derive an unexpectedly accurate approximation to π, simply because the fraction 355/113 happens to be so close to the correct value. But this is easily arranged. To do this, one should pick n as a multiple of 213, because then 113n/213 is an integer; one then drops n needles, and hopes for exactly x = 113n/213 successes.
If one drops 213 needles and happens to get 113 successes, then one can triumphantly report an estimate of π accurate to six decimal places. If not, one can just do 213 more trials and hope for a total of 226 successes; if not, just repeat as necessary. Lazzarini performed 3408 = 213 · 16 trials, making it seem likely that this is the strategy he used to obtain his "estimate".
External links
- Buffon's Needle at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Math Surprises: Buffon's Noodle at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- MSTE: Buffon's Needle
- Buffon's Needle Java Applet
- Estimating PI Visualization (Flash)
- Buffon's needle: fun and fundamentals (presentation) at slideshareSlideShareSlideShare is a Web 2.0 based slide hosting service. Users can upload files privately or publicly in the following file formats: PowerPoint, PDF, Keynote or OpenOffice presentations. Slide decks can then be viewed on the site itself, on hand held devices or embedded on other sites. Launched on...
- Animations for the Simulation of Buffon's Needle by Yihui Xie using the RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
package animation - 3D Physical Animation Java Applet by Jeffrey Ventrella