
Brunn-Minkowski theorem
Encyclopedia
In mathematics
, the Brunn–Minkowski theorem (or Brunn–Minkowski inequality) is an inequality relating the volumes (or more generally Lebesgue measure
s) of compact
subset
s of Euclidean space
. The original version of the Brunn–Minkowski theorem (Hermann Brunn
1887; Hermann Minkowski
1896) applied to convex sets; the generalization to compact nonconvex sets stated here is due to L.A. Lyusternik
(1935).
on Rn. Let A and B be two nonempty compact subsets of Rn. Then the following inequality holds:
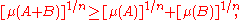
where A + B denotes the Minkowski sum:
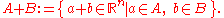
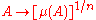
is concave
in the sense that, for every pair of nonempty compact subsets A and B of Rn and every 0 ≤ t ≤ 1,

For convex
sets A and B, the inequality in the theorem is strict
for 0 < t < 1 unless A and B are homothetic, i.e. are equal up to translation
and dilation
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Brunn–Minkowski theorem (or Brunn–Minkowski inequality) is an inequality relating the volumes (or more generally Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
s) of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The original version of the Brunn–Minkowski theorem (Hermann Brunn
Hermann Brunn
Karl Hermann Brunn was a German mathematician, known for his work in convex geometry and in knot theory .-Life and work:...
1887; Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
1896) applied to convex sets; the generalization to compact nonconvex sets stated here is due to L.A. Lyusternik
Lazar Lyusternik
Lazar Aronovich Lyusternik was a Soviet mathematician....
(1935).
Statement of the theorem
Let n ≥ 1 and let μ denote the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on Rn. Let A and B be two nonempty compact subsets of Rn. Then the following inequality holds:
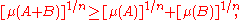
where A + B denotes the Minkowski sum:
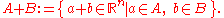
Remarks
The proof of the Brunn–Minkowski theorem establishes that the function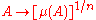
is concave
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
in the sense that, for every pair of nonempty compact subsets A and B of Rn and every 0 ≤ t ≤ 1,

For convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
sets A and B, the inequality in the theorem is strict
for 0 < t < 1 unless A and B are homothetic, i.e. are equal up to translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
and dilation
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
.
See also
- Isoperimetric inequality
- Milman's reverse Brunn–Minkowski inequality
- Minkowski–Steiner formula
- Prékopa–Leindler inequality
- Vitale's random Brunn–Minkowski inequality

