
Bose–Mesner algebra
Encyclopedia
In mathematics
, a Bose–Mesner algebra is a set of matrices
, together with set of rules (algebra) for combining (forming the products of) those matrices, such that certain conditions apply. Among these rules are:
Bose–Mesner algebras have applications in physics
to spin model
s, and in statistics
to the design of experiments
. They are named for R. C. Bose and Dale Marsh Mesner.
 consisting of all matrices
consisting of all matrices
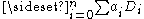 , with
, with  real [1] [2] [3].
real [1] [2] [3].
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Bose–Mesner algebra is a set of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, together with set of rules (algebra) for combining (forming the products of) those matrices, such that certain conditions apply. Among these rules are:
- the result of a product is also within the set of matrices
- there is an identity matrix in the set
- such that taking products is commutativeCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
.
Bose–Mesner algebras have applications in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
to spin model
Spin model
A spin model is a mathematical model used in physics primarily to explain magnetism. Spin models may either be classical or quantum mechanical in nature. Spin models have been studied in quantum field theory as examples of integrable models. Spin models are also used in quantum information theory...
s, and in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
to the design of experiments
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
. They are named for R. C. Bose and Dale Marsh Mesner.
Background
Consider the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
 consisting of all matrices
consisting of all matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
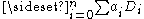 , with
, with  real [1] [2] [3].
real [1] [2] [3].-
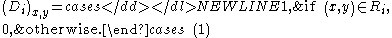
The definition of an association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
is equivalent to saying that the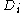 are
are 
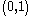 -matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
-matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which satisfy
- I.
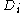 is symmetric,
is symmetric, - II.
 ,
, - III.
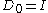 ,
, - IV.
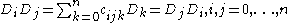 .
.
The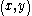 -th entry of the left side of
-th entry of the left side of 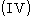 is the number of paths in the graph. Note that the rows and columns of
is the number of paths in the graph. Note that the rows and columns of 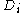 contain
contain 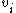
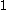 's:
's:
From , these matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, these matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
are symmetric. From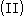 ,
,  are linearly independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
are linearly independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
, and the dimension of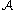 is
is 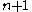 . From
. From 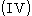 ,
, 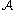 is closed under multiplication, and multiplication is always associative. This associativeAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
is closed under multiplication, and multiplication is always associative. This associativeAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
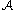 is called the Bose–Mesner algebra of the association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
is called the Bose–Mesner algebra of the association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
. Since the matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in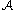 are symmetric and commute with each other, they can be simultaneously diagonalized. This means that there is a matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
are symmetric and commute with each other, they can be simultaneously diagonalized. This means that there is a matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
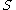 such that to each
such that to each  there is a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
there is a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
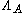 with
with 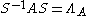 . This means that
. This means that 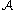 is semi-simple and has a unique basis of primitive idempotents
is semi-simple and has a unique basis of primitive idempotents  . These are real
. These are real 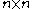 matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
satisfying
-
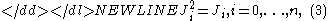
-
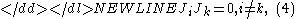
-
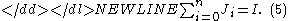
The Bose–Mesner algebra has two distinguished bases: the basis consisting of the adjacency matricesAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
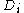 , and the basis consisting of the irreducible idempotent matricesIdempotent matrixIn algebra, an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix M is idempotent if and only if MM = M...
, and the basis consisting of the irreducible idempotent matricesIdempotent matrixIn algebra, an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix M is idempotent if and only if MM = M...
 . By definition, there exist well-defined complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. By definition, there exist well-defined complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s such that
-

-
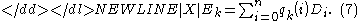
The p-numbers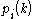 , and the q-numbers
, and the q-numbers 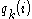 , play a prominent role in the theory [1]. They satisfy well-defined orthogonality relations. The p-numbers are the eigenvalues of the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
, play a prominent role in the theory [1]. They satisfy well-defined orthogonality relations. The p-numbers are the eigenvalues of the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
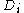 .
.
Theorem
The eigenvalues of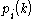 and
and  , satisfy the orthogonality conditions:
, satisfy the orthogonality conditions:
-
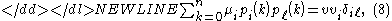
-
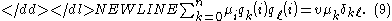
Also
-
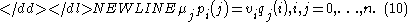
In matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
notation, these are
-
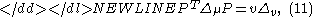
-
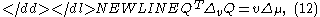
where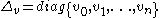 ,
, 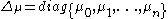 .
.
Proof of theorem
The eigenvalues of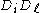 are
are 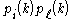 with multiplicities
with multiplicities 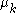 . This implies that
. This implies that
-
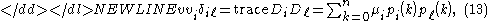
which proves Equation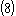 and Equation
and Equation 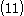 ,
,
-
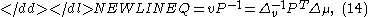
which gives Equations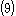 ,
, 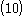 and
and 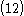 .
.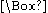
There is an analogy between extensions of association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
s and extensionsKronecker's theoremIn mathematics, Kronecker's theorem is either of two theorems named after Leopold Kronecker.- The existence of extension fields :This is a theorem stating that a polynomial in a field, p ∈ F[x], has a root in an extension field E \supset F.For example, a polynomial in the reals such...
of finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. The cases we are most interested in are those where the extended schemes are defined on the -th Cartesian power
-th Cartesian power 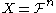 of a set
of a set 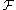 on which a basic association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
on which a basic association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
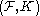 is defined. A first association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
is defined. A first association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
defined on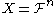 is called the
is called the  -th Kronecker powerKronecker productIn mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
-th Kronecker powerKronecker productIn mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
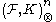 of
of 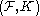 . Next the extension is defined on the same set
. Next the extension is defined on the same set 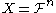 by gathering classes of
by gathering classes of 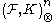 . The Kronecker powerKronecker productIn mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
. The Kronecker powerKronecker productIn mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
corresponds to the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
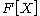 first defined on a fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
first defined on a fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
 , while the extension scheme corresponds to the extension field obtained as a quotient. An example of such an extended scheme is the Hamming schemeHamming schemeThe Hamming scheme, named after Richard Hamming, is also known as the hyper-cubic association scheme, and it is the most important example for coding theory...
, while the extension scheme corresponds to the extension field obtained as a quotient. An example of such an extended scheme is the Hamming schemeHamming schemeThe Hamming scheme, named after Richard Hamming, is also known as the hyper-cubic association scheme, and it is the most important example for coding theory...
.
Association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
s may be merged, but merging them leads to non-symmetric association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
s, whereas all usual codeCodeA code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
s are subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s in symmetric Abelian schemesAbelian varietyIn mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
[1] [2] [3].
-
-
-
-
-
-
-
-
-
-
-
- I.


