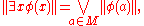Boolean-valued model
Encyclopedia
In mathematical logic
, a Boolean-valued model is a generalization of the ordinary Tarskian
notion of structure
from model theory
. In a Boolean-valued model, the truth values of proposition
s are not limited to "true" and "false", but instead take values in some fixed complete Boolean algebra
.
Boolean-valued models were introduced by Dana Scott
, Robert M. Solovay
, and Petr Vopěnka
in the 1960s in order to help understand Paul Cohen
's method of forcing
. They are also related to Heyting algebra semantics in intuitionistic logic
.
A Boolean-valued model for the language L consists of a universe M, which is a set of elements (or names), together with interpretations for the symbols. Specifically, the model must assign to each constant symbol of L an element of M, and to each n-ary function symbol f of L and each n-tuple <a0,...,an-1> of elements of M, the model must assign an element of M to the term f(a0,...,an-1).
Interpretation of the atomic formula
s of L is more complicated. To each pair a and b of elements of M, the model must assign a truth value ||a=b|| to the expression a=b; this truth value is taken from the Boolean algebra B. Similarly, for each n-ary relation symbol R of L and each n-tuple <a0,...,an-1> of elements of M, the model must assign an element of B to be the truth value ||R(a0,...,an-1)||.
is simply
The completeness of the Boolean algebra is required to define truth values for quantified formulas. If φ(x) is a formula with free variable x (and possibly other free variables that are suppressed), then
where the right-hand side is to be understood as the supremum
in B of the set of all truth values ||φ(a)|| as a ranges over M.
The truth value of a formula is sometimes referred to as its probability
. However, these are not probabilities in the ordinary sense, because they are not real number
s, but rather elements of the complete Boolean algebra B.
V. (Strictly speaking, VB is a proper class, so we need to reinterpret what it means to be a model
appropriately.) Informally, the elements of VB are "Boolean-valued sets". Given an ordinary set A, every set either is or is not a member; but given a Boolean-valued set, every set has a certain, fixed "probability" of being a member of A. Again, the "probability" is an element of B, not a real number. The concept of Boolean-valued sets resembles, but is not the same as, the notion of a fuzzy set
.
The ("probabilistic") elements of the Boolean-valued set, in turn, are also Boolean-valued sets, whose elements are also Boolean-valued sets, and so on. In order to obtain a non-circular definition of Boolean-valued set, they are defined inductively in a hierarchy similar to the cumulative hierarchy. For each ordinal α of V, the set VBα is defined as follows.
The class VB is defined to be the union of all sets VBα.
It is also possible to relativize this entire construction to some transitive model M of ZF (or sometimes a fragment thereof). The Boolean-valued model MB is obtained by applying the above construction inside M. The restriction to transitive models is not serious, as the Mostowski collapsing theorem
implies that every "reasonable" (well-founded, extensional) model is isomorphic to a transitive one. (If the model M is not transitive things get messier, as Ms interpretation of what it means to be a "function" or an "ordinal" may differ from the "external" interpretation.)
Once the elements of VB have been defined as above, it is necessary to define B-valued relations of equality and membership on VB. Here a B-valued relation on VB is a function from VB×VB to B. To avoid confusion with the usual equality and membership, these are denoted by ||x=y|| and ||x∈y|| for x and y in VB. They are defined as follows:
The symbols ∑ and ∏ denote the least upper bound and greatest lower bound operations, respectively, in the complete Boolean algebra B. At first sight the definitions above appear to be circular: || ∈ || depends on || = ||, which depends on || ⊆ ||, which depends on || ∈ ||. However, a close examination shows that the definition of || ∈ || only depends on || ∈ || for elements of smaller rank, so || ∈ || and || = || are well defined functions from VB×VB to B.
It can be shown that the B-valued relations || ∈ || and || = || on VB make VB into a Boolean-valued model of set theory. Each sentence of first order set theory with no free variables has a truth value in B; it must be shown that the axioms for equality and all the axioms of ZF set theory (written without free variables) have truth value 1 (the largest element of B). This proof is straightforward, but it is long because there are many different axioms that need to be checked.
to obtain independence results
and to construct models of set theory for other purposes. The method was originally developed by Paul Cohen
but has been greatly extended since then. In one form, forcing "adds to the universe" a generic
subset of a poset, the poset being designed to impose interesting properties on the newly-added object. The wrinkle is that (for interesting posets) it can be proved that there simply is no such generic subset of the poset. There are three usual ways of dealing with this:
on P is generated by cones (sets of the form {q|q≤p}, for fixed p). (Other approaches to constructing B are discussed below.)
Now the order on B (after removing the zero element) can replace P for forcing purposes, and the forcing relation can be interpreted semantically by saying that, for p an element of B and φ a formula of the forcing language,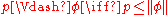
where ||φ|| is the truth value of φ in VB.
This approach succeeds in assigning a semantics to forcing over V without resorting to fictional generic objects. The disadvantages are that the semantics is not 2-valued, and that the combinatorics of B are often more complicated than those of the underlying poset P.
We now explain these steps in more detail.
For any poset P there is a complete Boolean algebra B and a map e from P to B+ (the non-zero elements of B) such that the image is dense, e(p)≤e(q) whenever p≤q, and e(p)e(q)=0 whenever p and q are incompatible. This Boolean algebra is unique up to isomorphism. It can be constructed as the algebra of regular open sets in the topological space of P (with underlying set P, and a base given by the sets Up of elements q with q≤p).
The map from the poset P to the complete Boolean algebra B is not injective in general. The map is injective if and only if P has the following property: if every r≤p is compatible with q, then p≤q.
The ultrafilter U on B is defined to be the set of elements b of B that are greater than some element of (the image of) G. Given an ultrafilter U on a Boolean algebra, we get a homomorphism to {true, false}
by mapping U to true and its complement to false. Conversely, given such a homomorphism, the inverse image of true is an ultrafilter, so ultrafilters are essentially the same as homomorphisms to {true, false}. (Algebraists might prefer to use maximal ideals instead of ultrafilters: the complement of an ultrafilter is a maximal ideal, and conversely the complement of a maximal ideal is an ultrafilter.)
If g is a homomorphism from a Boolean algebra B to a Boolean algebra C and MB is any
B-valued model of ZF (or of any other theory for that matter) we can turn MB into a C -valued model by applying the homomorphism g to the value of all formulas. In particular if C is {true, false} we get a {true, false}-valued model. This is almost the same as an ordinary model: in fact we get an ordinary model on the set of equivalence classes under || = || of a {true, false}-valued model. So we get an ordinary model of ZF set theory by starting from M, a Boolean algebra B, and an ultrafilter U on B.
(The model of ZF constructed like this is not transitive. In practice one applies the Mostowski collapsing theorem
to turn this into a transitive model.)
We have seen that forcing can be done using Boolean-valued models, by constructing a Boolean algebra with ultrafilter from a poset with a generic subset. It is also possible to go back the other way: given a Boolean algebra B, we can form a poset P of all the nonzero elements of B, and a generic ultrafilter on B restricts to a generic set on P. So the techniques of forcing and Boolean-valued models are essentially equivalent.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a Boolean-valued model is a generalization of the ordinary Tarskian
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
notion of structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
from model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
. In a Boolean-valued model, the truth values of proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s are not limited to "true" and "false", but instead take values in some fixed complete Boolean algebra
Complete Boolean algebra
In mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum . Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing...
.
Boolean-valued models were introduced by Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
, Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
, and Petr Vopěnka
Petr Vopenka
Petr Vopěnka is a Czech mathematician. In the early seventies, he established the Alternative Set Theory , which he subsequently developed in a series of articles and monographs...
in the 1960s in order to help understand Paul Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
's method of forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
. They are also related to Heyting algebra semantics in intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
.
Definition
Fix a complete Boolean algebra B and a first-order language L; the signature of L will consist of a collection of constant symbols, function symbols, and relation symbols.A Boolean-valued model for the language L consists of a universe M, which is a set of elements (or names), together with interpretations for the symbols. Specifically, the model must assign to each constant symbol of L an element of M, and to each n-ary function symbol f of L and each n-tuple <a0,...,an-1> of elements of M, the model must assign an element of M to the term f(a0,...,an-1).
Interpretation of the atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s of L is more complicated. To each pair a and b of elements of M, the model must assign a truth value ||a=b|| to the expression a=b; this truth value is taken from the Boolean algebra B. Similarly, for each n-ary relation symbol R of L and each n-tuple <a0,...,an-1> of elements of M, the model must assign an element of B to be the truth value ||R(a0,...,an-1)||.
Interpretation of other formulas and sentences
The truth values of the atomic formulas can be used to reconstruct the truth values of more complicated formulas, using the structure of the Boolean algebra. For propositional connectives, this is easy; one simply applies the corresponding Boolean operators to the truth values of the subformulae. For example, if φ(x) and ψ(y,z) are formulas with one and two free variables, respectively, and if a, b, c are elements of the model's universe to be substituted for x, y, and z, then the truth value ofis simply
The completeness of the Boolean algebra is required to define truth values for quantified formulas. If φ(x) is a formula with free variable x (and possibly other free variables that are suppressed), then
where the right-hand side is to be understood as the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
in B of the set of all truth values ||φ(a)|| as a ranges over M.
The truth value of a formula is sometimes referred to as its probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. However, these are not probabilities in the ordinary sense, because they are not real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, but rather elements of the complete Boolean algebra B.
Boolean-valued models of set theory
Given a complete Boolean algebra B there is a Boolean-valued model denoted by VB, which is the Boolean-valued analogue of the von Neumann universeVon Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
V. (Strictly speaking, VB is a proper class, so we need to reinterpret what it means to be a model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
appropriately.) Informally, the elements of VB are "Boolean-valued sets". Given an ordinary set A, every set either is or is not a member; but given a Boolean-valued set, every set has a certain, fixed "probability" of being a member of A. Again, the "probability" is an element of B, not a real number. The concept of Boolean-valued sets resembles, but is not the same as, the notion of a fuzzy set
Fuzzy set
Fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to...
.
The ("probabilistic") elements of the Boolean-valued set, in turn, are also Boolean-valued sets, whose elements are also Boolean-valued sets, and so on. In order to obtain a non-circular definition of Boolean-valued set, they are defined inductively in a hierarchy similar to the cumulative hierarchy. For each ordinal α of V, the set VBα is defined as follows.
- VB0 is the empty set.
- VBα+1 is the set of all functions from VBα to B. (Such a function represents a "probabilistic" subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of VBα; if f is such a function, then for any x∈VBα, f(x) is the probability that x is in the set.) - If α is a limit ordinal, VBα is the union of VBβ for β<α
The class VB is defined to be the union of all sets VBα.
It is also possible to relativize this entire construction to some transitive model M of ZF (or sometimes a fragment thereof). The Boolean-valued model MB is obtained by applying the above construction inside M. The restriction to transitive models is not serious, as the Mostowski collapsing theorem
Mostowski collapse
In mathematical logic, the Mostowski collapse lemma is a statement in set theory named for Andrzej Mostowski.-Statement:Suppose that R is a binary relation on a class X such that...
implies that every "reasonable" (well-founded, extensional) model is isomorphic to a transitive one. (If the model M is not transitive things get messier, as Ms interpretation of what it means to be a "function" or an "ordinal" may differ from the "external" interpretation.)
Once the elements of VB have been defined as above, it is necessary to define B-valued relations of equality and membership on VB. Here a B-valued relation on VB is a function from VB×VB to B. To avoid confusion with the usual equality and membership, these are denoted by ||x=y|| and ||x∈y|| for x and y in VB. They are defined as follows:
- ||x∈y|| is defined to be ∑t∈Dom(y) ||x=t|| ∧ y(t) ("x is in y if it is equal to something in y").
- ||x=y|| is defined to be ||x⊆y||∧||y⊆x|| ("x equals y if x and y are both subsets of each other"), where
- ||x⊆y|| is defined to be ∏t∈Dom(x) x(t)⇒||t∈y|| ("x is a subset of y if all elements of x are in y")
The symbols ∑ and ∏ denote the least upper bound and greatest lower bound operations, respectively, in the complete Boolean algebra B. At first sight the definitions above appear to be circular: || ∈ || depends on || = ||, which depends on || ⊆ ||, which depends on || ∈ ||. However, a close examination shows that the definition of || ∈ || only depends on || ∈ || for elements of smaller rank, so || ∈ || and || = || are well defined functions from VB×VB to B.
It can be shown that the B-valued relations || ∈ || and || = || on VB make VB into a Boolean-valued model of set theory. Each sentence of first order set theory with no free variables has a truth value in B; it must be shown that the axioms for equality and all the axioms of ZF set theory (written without free variables) have truth value 1 (the largest element of B). This proof is straightforward, but it is long because there are many different axioms that need to be checked.
Relationship to forcing
Set theorists use a technique called forcingForcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
to obtain independence results
Independence (mathematical logic)
In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...
and to construct models of set theory for other purposes. The method was originally developed by Paul Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
but has been greatly extended since then. In one form, forcing "adds to the universe" a generic
Generic filter
In the mathematical field of set theory, a generic filter is a kind of object used in the theory of forcing, a technique used for many purposes, but especially to establish the independence of certain propositions from certain formal theories, such as ZFC...
subset of a poset, the poset being designed to impose interesting properties on the newly-added object. The wrinkle is that (for interesting posets) it can be proved that there simply is no such generic subset of the poset. There are three usual ways of dealing with this:
- syntactic forcing A forcing relation
 is defined between elements p of the poset and formulas φ of the forcing language. This relation is defined syntactically and has no semantics; that is, no model is ever produced. Rather, starting with the assumption that ZFC (or some other axiomatization of set theory) proves the independent statement, one shows that ZFC must also be able to prove a contradiction. However, the forcing is "over V"; that is, it is not necessary to start with a countable transitive model. See Kunen (1980) for an exposition of this method.
is defined between elements p of the poset and formulas φ of the forcing language. This relation is defined syntactically and has no semantics; that is, no model is ever produced. Rather, starting with the assumption that ZFC (or some other axiomatization of set theory) proves the independent statement, one shows that ZFC must also be able to prove a contradiction. However, the forcing is "over V"; that is, it is not necessary to start with a countable transitive model. See Kunen (1980) for an exposition of this method. - countable transitive models One starts with a countableCountable setIn mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
transitiveTransitive setIn set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
model M of as much of set theory as is needed for the desired purpose, and that contains the poset. Then there do exist filters on the poset that are generic over M; that is, that meet all dense open subsets of the poset that happen also to be elements of M. - fictional generic objects Commonly, set theorists will simply pretend that the poset has a subset that is generic over all of V. This generic object, in nontrivial cases, cannot be an element of V, and therefore "does not really exist". (Of course, it is a point of philosophical contention whether any sets "really exist", but that is outside the scope of the current discussion.) Perhaps surprisingly, with a little practice this method is useful and reliable, but it can be philosophically unsatisfying.
Boolean-valued models and syntactic forcing
Boolean-valued models can be used to give semantics to syntactic forcing; the price paid is that the semantics is not 2-valued ("true or false"), but assigns truth values from some complete Boolean algebra. Given a forcing poset P, there is a corresponding complete Boolean algebra B, often obtained as the collection of regular open subsets of P, where the topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on P is generated by cones (sets of the form {q|q≤p}, for fixed p). (Other approaches to constructing B are discussed below.)
Now the order on B (after removing the zero element) can replace P for forcing purposes, and the forcing relation can be interpreted semantically by saying that, for p an element of B and φ a formula of the forcing language,
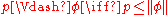
where ||φ|| is the truth value of φ in VB.
This approach succeeds in assigning a semantics to forcing over V without resorting to fictional generic objects. The disadvantages are that the semantics is not 2-valued, and that the combinatorics of B are often more complicated than those of the underlying poset P.
Boolean-valued models and generic objects over countable transitive models
One interpretation of forcing starts with a countable transitive model M of ZF set theory, a partially ordered set P, and a "generic" subset G of P, and constructs a new model of ZF set theory from these objects. (The conditions that the model be countable and transitive simplify some technical problems, but are not essential.) Cohen's construction can be carried out using Boolean-valued models as follows.- Construct a complete Boolean algebra B as the complete Boolean algebra "generated by" the poset P.
- Construct an ultrafilter U on B (or equivalently a homomorphism from B to the Boolean algebra {true, false}) from the generic subset G of P.
- Use the homomorphism from B to {true, false} to turn the Boolean-valued model MB of the section above into an ordinary model of ZF.
We now explain these steps in more detail.
For any poset P there is a complete Boolean algebra B and a map e from P to B+ (the non-zero elements of B) such that the image is dense, e(p)≤e(q) whenever p≤q, and e(p)e(q)=0 whenever p and q are incompatible. This Boolean algebra is unique up to isomorphism. It can be constructed as the algebra of regular open sets in the topological space of P (with underlying set P, and a base given by the sets Up of elements q with q≤p).
The map from the poset P to the complete Boolean algebra B is not injective in general. The map is injective if and only if P has the following property: if every r≤p is compatible with q, then p≤q.
The ultrafilter U on B is defined to be the set of elements b of B that are greater than some element of (the image of) G. Given an ultrafilter U on a Boolean algebra, we get a homomorphism to {true, false}
by mapping U to true and its complement to false. Conversely, given such a homomorphism, the inverse image of true is an ultrafilter, so ultrafilters are essentially the same as homomorphisms to {true, false}. (Algebraists might prefer to use maximal ideals instead of ultrafilters: the complement of an ultrafilter is a maximal ideal, and conversely the complement of a maximal ideal is an ultrafilter.)
If g is a homomorphism from a Boolean algebra B to a Boolean algebra C and MB is any
B-valued model of ZF (or of any other theory for that matter) we can turn MB into a C -valued model by applying the homomorphism g to the value of all formulas. In particular if C is {true, false} we get a {true, false}-valued model. This is almost the same as an ordinary model: in fact we get an ordinary model on the set of equivalence classes under || = || of a {true, false}-valued model. So we get an ordinary model of ZF set theory by starting from M, a Boolean algebra B, and an ultrafilter U on B.
(The model of ZF constructed like this is not transitive. In practice one applies the Mostowski collapsing theorem
Mostowski collapse
In mathematical logic, the Mostowski collapse lemma is a statement in set theory named for Andrzej Mostowski.-Statement:Suppose that R is a binary relation on a class X such that...
to turn this into a transitive model.)
We have seen that forcing can be done using Boolean-valued models, by constructing a Boolean algebra with ultrafilter from a poset with a generic subset. It is also possible to go back the other way: given a Boolean algebra B, we can form a poset P of all the nonzero elements of B, and a generic ultrafilter on B restricts to a generic set on P. So the techniques of forcing and Boolean-valued models are essentially equivalent.