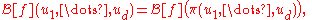Blossom (functional)
Encyclopedia
In numerical analysis
, a blossom is a functional
that can be applied to any polynomial
, but is mostly used for Bézier
and spline
curves and surfaces.
The blossom of a polynomial ƒ, often denoted
is completely characterised by the three properties:
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, a blossom is a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
that can be applied to any polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, but is mostly used for Bézier
Bézier curve
A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
and spline
Spline
Spline can refer to:* Spline , a mating feature for rotating elements* Spline , a mathematical function used for interpolation or smoothing* Smoothing spline, a method of smoothing using a spline function...
curves and surfaces.
The blossom of a polynomial ƒ, often denoted
is completely characterised by the three properties:
- It is a symmetric function of its arguments:
-
-
- (where π is any permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of its arguments).- It is affine in each of its arguments:
-
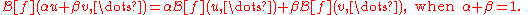
- It satisfies the diagonal property:
-
