Bispherical coordinates
Encyclopedia
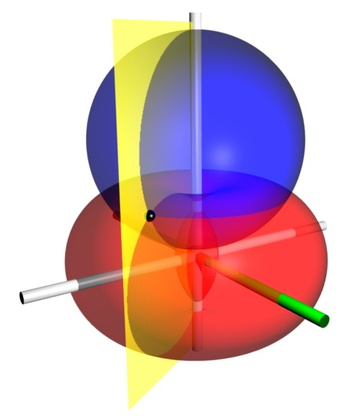
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
that results from rotating the two-dimensional bipolar coordinate system
Bipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
about the axis that connects the two foci. Thus, the two foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
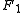and 
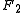in bipolar coordinatesBipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
remain points (on the
-axis, the axis of rotation) in the bispherical coordinate system.Definition
The most common definition of bispherical coordinates
is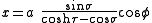
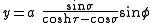
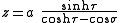
where the
coordinate of a point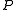 
equals the angle 
and the 
coordinate equals the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the ratio of the distances
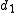and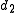 
to the foci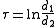
Coordinate surfaces
Surfaces of constant
correspond to intersecting tori of different radii
that all pass through the foci but are not concentric. The surfaces of constant
are non-intersecting spheres of different radii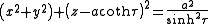
that surround the foci. The centers of the constant-
spheres lie along the 
-axis, whereas the constant-
tori are centered in the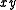 
plane.Scale factors
The scale factors for the bispherical coordinates
and 
are equal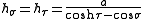
whereas the azimuthal scale factor equals
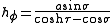
Thus, the infinitesimal volume element equals
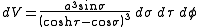
and the Laplacian is given by
Other differential operators such as
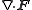and 
can be expressed in the coordinates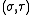 
by substituting the scale factors into the general formulae found in orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Applications
The classic applications of bispherical coordinates are in solving partial differential equations,e.g., Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
, for which bispherical coordinates allow a
separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. However, the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
is not separable in bispherical coordinates. A typical example would be the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
surrounding two conducting spheres of different radii.