
Binomial regression
Encyclopedia
In statistics
, binomial regression is a technique in which the response (often referred to as Y) is the result of a series of Bernoulli trial
s, or a series of one of two possible disjoint outcomes (traditionally denoted "success" or 1, and "failure" or 0). In binomial regression, the probability of a success is related to explanatory variables: the corresponding concept in ordinary regression is to relate the mean value of the unobserved response to explanatory variables.
A binomial regression model is a special case of a generalized linear model
.
of the predictions is then given by

where 1A is the indicator function which takes on the value one when the event A occurs, and zero otherwise: in this formulation, for any given observation yi, only one of the two terms inside the product contributes, according to whether yi=0 or 1. The likelihood function is more fully specified by defining the formal parameters μi as parameterised functions of the explanatory variables: this defines the likelihood in terms of a much reduced number of parameters. Fitting of the model is usually achieved by employing the method of maximum likelihood
to determine these parameters. In practice, the use of a formulation as a generalised linear model allows advantage to be taken of certain algorithmic ideas which are applicable across the whole class of more general models but which do not apply to all maximum likelihood problems.
Models used in binomial regression can often be extended to multinomial data.
There are many methods of generating the values of μ in systematic ways that allow for interpretation of the model; they are discussed below.

Here η is an intermediate variable representing a linear combination, containing the regression parameters, of the explanatory variables. The function
g is the cumulative distribution function
(cdf) of some probability distribution
. Usually this probability distribution has a range from minus infinity to plus infinity so that any finite value of η is transformed by the function g to a value inside the range 0 to 1.
In the case of logistic regression
, the link function is the log of the odds ratio or logistic function
. In the case of probit
, the link is the cdf of the normal distribution. The linear probability model is not a proper binomial regression specification because predictions need not be in the range of zero to one, it is sometimes used for this type of data when the probability space is where interpretation occurs or when the analyst lacks sufficient sophistication to fit or calculate approximate linearizations of probabilities for interpretation.
involving a binomial observed variable Y can be constructed such that Y is related to the latent variable Y* via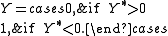
The latent variable Y* is then related to a set of regression variables X by the model
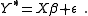
This results in a binomial regression model.
The variance of can not be identified and when it is not of interest is often assumed to be equal to one. If is normally distributed, then a probit is the appropriate model and if is log-Weibull distributed, then a logit is appropriate. If is uniformly distributed, then a linear probability model is appropriate.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, binomial regression is a technique in which the response (often referred to as Y) is the result of a series of Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s, or a series of one of two possible disjoint outcomes (traditionally denoted "success" or 1, and "failure" or 0). In binomial regression, the probability of a success is related to explanatory variables: the corresponding concept in ordinary regression is to relate the mean value of the unobserved response to explanatory variables.
A binomial regression model is a special case of a generalized linear model
Generalized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
.
Example application
In one published example of an application of binomial regression, the details were as follows. The observed outcome variable was whether or not a fault occurred in an industrial process. There were two explanatory variables: the first was a simple two-case factor representing whether or not a modified version of the process was used and the second was an ordinary quantitative variable measuring the purity of the material being supplied for the process.Specification of model
The results are assumed to be binomially distributed. They are often fitted as a generalised linear model where the predicted values μ are the probabilities that any individual event will result in a success. The likelihoodLikelihood
Likelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
of the predictions is then given by

where 1A is the indicator function which takes on the value one when the event A occurs, and zero otherwise: in this formulation, for any given observation yi, only one of the two terms inside the product contributes, according to whether yi=0 or 1. The likelihood function is more fully specified by defining the formal parameters μi as parameterised functions of the explanatory variables: this defines the likelihood in terms of a much reduced number of parameters. Fitting of the model is usually achieved by employing the method of maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
to determine these parameters. In practice, the use of a formulation as a generalised linear model allows advantage to be taken of certain algorithmic ideas which are applicable across the whole class of more general models but which do not apply to all maximum likelihood problems.
Models used in binomial regression can often be extended to multinomial data.
There are many methods of generating the values of μ in systematic ways that allow for interpretation of the model; they are discussed below.
Link functions
There is a requirement that the modelling linking the probabilities μ to the explanatory variables should be of a form which only produces values in the range 0 to 1. Many models can be fitted into the form
Here η is an intermediate variable representing a linear combination, containing the regression parameters, of the explanatory variables. The function
g is the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(cdf) of some probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. Usually this probability distribution has a range from minus infinity to plus infinity so that any finite value of η is transformed by the function g to a value inside the range 0 to 1.
In the case of logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
, the link function is the log of the odds ratio or logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
. In the case of probit
Probit model
In statistics, a probit model is a type of regression where the dependent variable can only take two values, for example married or not married....
, the link is the cdf of the normal distribution. The linear probability model is not a proper binomial regression specification because predictions need not be in the range of zero to one, it is sometimes used for this type of data when the probability space is where interpretation occurs or when the analyst lacks sufficient sophistication to fit or calculate approximate linearizations of probabilities for interpretation.
Latent variable interpretation / derivation
A latent variable modelLatent variable model
A latent variable model is a statistical model that relates a set of variables to a set of latent variables.It is assumed that 1) the responses on the indicators or manifest variables are the result of...
involving a binomial observed variable Y can be constructed such that Y is related to the latent variable Y* via
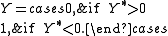
The latent variable Y* is then related to a set of regression variables X by the model
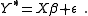
This results in a binomial regression model.
The variance of can not be identified and when it is not of interest is often assumed to be equal to one. If is normally distributed, then a probit is the appropriate model and if is log-Weibull distributed, then a logit is appropriate. If is uniformly distributed, then a linear probability model is appropriate.

