
Biharmonic equation
Encyclopedia
In mathematics
, the biharmonic equation is a fourth-order partial differential equation
which arises in areas of continuum mechanics
, including linear elasticity
theory and the solution of Stokes flows. It is written as
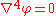
or
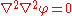
or

where is the fourth power of the del
is the fourth power of the del
operator and the square of the laplacian operator (or
(or  ), and it is known as the biharmonic operator or the bilaplacian operator.
), and it is known as the biharmonic operator or the bilaplacian operator.
For example, in three dimensional cartesian coordinates the biharmonic equation has the form
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the biharmonic equation is a fourth-order partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
which arises in areas of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, including linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
theory and the solution of Stokes flows. It is written as
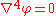
or
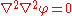
or

where
 is the fourth power of the del
is the fourth power of the delDel
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator and the square of the laplacian operator
 (or
(or  ), and it is known as the biharmonic operator or the bilaplacian operator.
), and it is known as the biharmonic operator or the bilaplacian operator.For example, in three dimensional cartesian coordinates the biharmonic equation has the form
-
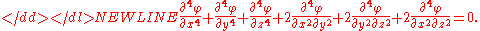
As another example, in n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
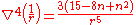
where
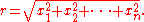
which, for n=3 and n=5 only, becomes the biharmonic equation.
A solution to the biharmonic equation is called a biharmonic function. Any harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
is biharmonic, but the converse is not always true.
In polar coordinates, the biharmonic equation is
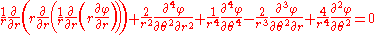
which can be solved by separation of variables. The result is the Michell solutionMichell solutionThe Michell solution is a general solution to the elasticity equations in polar coordinates . The solution is such that the stress components are in the form of a Fourier series in \theta \, ....
.
2 dimensional space
The general solution to the 2 dimensional case is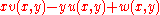
where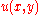 ,
, 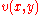 and
and 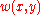 are harmonic functions and
are harmonic functions and 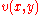 is a harmonic conjugateHarmonic conjugateIn mathematics, a function u defined on some open domain \Omega\subset\R^2 is said to have as a conjugate a function v if and only if they are respectively real and imaginary part of a holomorphic function f of the complex variable z:=x+iy\in\Omega. That is, v is conjugated to u if f:=u+iv is...
is a harmonic conjugateHarmonic conjugateIn mathematics, a function u defined on some open domain \Omega\subset\R^2 is said to have as a conjugate a function v if and only if they are respectively real and imaginary part of a holomorphic function f of the complex variable z:=x+iy\in\Omega. That is, v is conjugated to u if f:=u+iv is...
of .
.
Just as harmonic functions in 2 variables are closely related to complex analytic functions, so are biharmonic functions in 2 variables. The general form of a biharmonic function in 2 variables can also be written as
where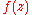 and
and  are analytic functions.
are analytic functions.

