Baire function
Encyclopedia
In mathematics
, Baire functions are certain sets of function
s. They are studied in several fields of mathematics, including real analysis
and
topology
.
Baire functions of class n, for any ordinal number
n, are a set of real-valued functions defined on the real line, as follows.
Many important functions in analysis which are not continuous are of Baire class one. For instance, the derivative
of any differentiable function is either continuous (class 0) or class 1.
Henri Lebesgue
proved that each Baire class is non-empty, and that there exist functions which are not in any Baire class.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Baire functions are certain sets of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. They are studied in several fields of mathematics, including real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
and
topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Baire functions of class n, for any ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
n, are a set of real-valued functions defined on the real line, as follows.
- The Baire class 0 functions are the continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s.
- The Baire class 1 functions are those functions which are the pointwise limitPointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
of a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of Baire class 0 functions, but are not of Baire class 0.
- In general, the Baire class n functions are all functions which are the pointwise limit of a sequence of functions each of which has Baire class less than n, but do not themselves appear in any lower-numbered class.
Many important functions in analysis which are not continuous are of Baire class one. For instance, the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of any differentiable function is either continuous (class 0) or class 1.
Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
proved that each Baire class is non-empty, and that there exist functions which are not in any Baire class.
- An example of a Baire class two function on the interval [0,1] is the characteristic function of the rational numbers,
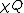, also known as the Dirichlet function. It is discontinuous everywhere. However, if you restrict its domain to the irrational numbers, it is continuous. This demonstrates the fact that as n increases, Baire-n functions are more discontinuous.
- An important theorem in the theory of Baire function is the Baire Characterisation Theorem. It states that a real valued function f defined on a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X is a Baire-1 function if and only if for every non-empty closed subset K of X, the restriction of f to K has a point of continuity relative to the topology of K.