Babylonian numerals
Encyclopedia
Babylonian numerals were written in cuneiform, using a wedge-tipped reed
stylus
to make a mark on a soft clay
tablet which would be exposed in the sun
to harden to create a permanent record.
The Babylonians, who were famous for their astronomical observations and calculations (aided by their invention of the abacus
), used a sexagesimal (base-60) positional numeral system
inherited from the Sumer
ian and also Akkad
ian civilizations. Neither of the predecessors was a positional system (having a convention for which ‘end’ of the numeral represented the units).
This system first appeared around 3100 B.C. It is also credited as being the first known positional numeral system, in which the value of a particular digit depends both on the digit itself and its position within the number. This was an extremely important development, because non-place-value systems require unique symbols to represent each power of a base (ten, one hundred, one thousand, and so forth), making calculations difficult.
Only two symbols (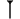
to count units and 
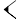to count tens) were used to notate the 59 non-zero digit
s. These symbols and their values were combined to form a digit in a sign-value notation
way similar to that of Roman numerals
; for example, the combination
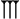represented the digit for 23 (see table of digits below). A space was left to indicate a place without value, similar to the modern-day zero
. Babylonians later devised a sign to represent this empty place. They lacked a symbol to serve the function of radix point
, so the place of the units had to be inferred from context : 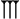could have represented 23 or 23×60 or 23×60×60 or 23/60, etc.
Their system clearly used internal decimal
to represent digits, but it was not really a mixed-radix
system of bases 10 and 6, since the ten sub-base was used merely to facilitate the representation of the large set of digits needed, while the place-values in a digit string were consistently 60-based and the arithmetic
needed to work with these digit strings was correspondingly sexagesimal.
The legacy of sexagesimal still survives to this day, in the form of degree
s (360° in a circle
or 60° in an angle
of an equilateral triangle), minute
s, and second
s in trigonometry
and the measurement of time
, although both of these systems are actually mixed radix.
A common theory is that 60
, a superior highly composite number
(the previous and next in the series being 12
and 120
), was chosen due to its prime factorization: 2×2×3×5, which makes it divisible by 1, 2, 3, 4, 5, 6, 10
, 12
, 15
, 20
, and 30
. In fact, it is the smallest integer divisible by all integers from 1 to 6. Integer
s and fraction
s were represented identically — a radix point was not written but rather made clear by context.
. Although they understood the idea of nothingness, it was not seen as a number—merely the lack of a number. What the Babylonians had instead was a space (and later a disambiguating placeholder symbol ) to mark the nonexistence of a digit in a certain place value.
Phragmites
Phragmites, the Common reed, is a large perennial grass found in wetlands throughout temperate and tropical regions of the world. Phragmites australis is sometimes regarded as the sole species of the genus Phragmites, though some botanists divide Phragmites australis into three or four species...
stylus
Stylus
A stylus is a writing utensil, or a small tool for some other form of marking or shaping, for example in pottery. The word is also used for a computer accessory . It usually refers to a narrow elongated staff, similar to a modern ballpoint pen. Many styli are heavily curved to be held more easily...
to make a mark on a soft clay
Clay
Clay is a general term including many combinations of one or more clay minerals with traces of metal oxides and organic matter. Geologic clay deposits are mostly composed of phyllosilicate minerals containing variable amounts of water trapped in the mineral structure.- Formation :Clay minerals...
tablet which would be exposed in the sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
to harden to create a permanent record.
The Babylonians, who were famous for their astronomical observations and calculations (aided by their invention of the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
), used a sexagesimal (base-60) positional numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
inherited from the Sumer
Sumer
Sumer was a civilization and historical region in southern Mesopotamia, modern Iraq during the Chalcolithic and Early Bronze Age....
ian and also Akkad
Akkad
The Akkadian Empire was an empire centered in the city of Akkad and its surrounding region in Mesopotamia....
ian civilizations. Neither of the predecessors was a positional system (having a convention for which ‘end’ of the numeral represented the units).
This system first appeared around 3100 B.C. It is also credited as being the first known positional numeral system, in which the value of a particular digit depends both on the digit itself and its position within the number. This was an extremely important development, because non-place-value systems require unique symbols to represent each power of a base (ten, one hundred, one thousand, and so forth), making calculations difficult.
Only two symbols (
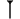
Digit
Digit may refer to:* Digit , one of several most distal parts of a limb—fingers, thumbs, and toes on hands and feet* Numerical digit, as used in mathematics or computer science* Hexadecimal, representing a four-bit number...
s. These symbols and their values were combined to form a digit in a sign-value notation
Sign-value notation
A sign-value notation represents numbers by a series of numeric signs that added together equal the number represented. In Roman numerals for example, X means ten and L means fifty. Hence LXXX means eighty . There is no need for zero in sign-value notation...
way similar to that of Roman numerals
Roman numerals
The numeral system of ancient Rome, or Roman numerals, uses combinations of letters from the Latin alphabet to signify values. The numbers 1 to 10 can be expressed in Roman numerals as:...
; for example, the combination
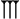
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Babylonians later devised a sign to represent this empty place. They lacked a symbol to serve the function of radix point
Radix point
In mathematics and computing, a radix point is the symbol used in numerical representations to separate the integer part of a number from its fractional part . "Radix point" is a general term that applies to all number bases...
, so the place of the units had to be inferred from context :
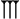
Their system clearly used internal decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
to represent digits, but it was not really a mixed-radix
Mixed radix
Mixed radix numeral systems are non-standard positional numeral systems in which the numerical base varies from position to position. Such numerical representation applies when a quantity is expressed using a sequence of units that are each a multiple of the next smaller one, but not by the same...
system of bases 10 and 6, since the ten sub-base was used merely to facilitate the representation of the large set of digits needed, while the place-values in a digit string were consistently 60-based and the arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
needed to work with these digit strings was correspondingly sexagesimal.
The legacy of sexagesimal still survives to this day, in the form of degree
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
s (360° in a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
or 60° in an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
of an equilateral triangle), minute
Minute
A minute is a unit of measurement of time or of angle. The minute is a unit of time equal to 1/60th of an hour or 60 seconds. In the UTC time scale, a minute on rare occasions has 59 or 61 seconds; see leap second. The minute is not an SI unit; however, it is accepted for use with SI units...
s, and second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s in trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
and the measurement of time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, although both of these systems are actually mixed radix.
A common theory is that 60
60 (number)
60 is the natural number following 59 and preceding 61. Being three times twenty, 60 is called "three score" in some older literature.-In mathematics:...
, a superior highly composite number
Superior highly composite number
In mathematics, a superior highly composite number is a certain kind of natural number with the following properties. A natural number n is called superior highly composite if there is an ε > 0 such that for all natural numbers k ≥ 1,...
(the previous and next in the series being 12
12 (number)
12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
and 120
120 (number)
120 is the natural number following 119 and preceding 121. 120 was known as "the great hundred", especially prior to the year 1700, from the Teutonic Hundert which equalled 120. The number 100, now known commonly as "one hundred" was then known as "the small hundred". It is also known as...
), was chosen due to its prime factorization: 2×2×3×5, which makes it divisible by 1, 2, 3, 4, 5, 6, 10
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 12
12 (number)
12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
, 15
15 (number)
15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, 20
20 (number)
20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems....
, and 30
30 (number)
30 is the natural number following 29 and preceding 31.-In mathematics:30 is the sum of the first four squares, which makes it a square pyramidal number.It is a primorial and is the smallest Giuga number....
. In fact, it is the smallest integer divisible by all integers from 1 to 6. Integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
s were represented identically — a radix point was not written but rather made clear by context.
Numerals
The Babylonians did not technically have a digit for, nor a concept of, the number zero0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Although they understood the idea of nothingness, it was not seen as a number—merely the lack of a number. What the Babylonians had instead was a space (and later a disambiguating placeholder symbol ) to mark the nonexistence of a digit in a certain place value.
See also
- BabyloniaBabyloniaBabylonia was an ancient cultural region in central-southern Mesopotamia , with Babylon as its capital. Babylonia emerged as a major power when Hammurabi Babylonia was an ancient cultural region in central-southern Mesopotamia (present-day Iraq), with Babylon as its capital. Babylonia emerged as...
- BabylonBabylonBabylon was an Akkadian city-state of ancient Mesopotamia, the remains of which are found in present-day Al Hillah, Babil Province, Iraq, about 85 kilometers south of Baghdad...
- History of zero
- Numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
External links
- Babylonian numerals
- Cuneiform numbers
- Babylonian Mathematics
- High resolution photographs, descriptions, and analysis of the root(2) tablet (YBC 7289) from the Yale Babylonian Collection
- Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection
- Babylonian Numerals by Michael Schreiber, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.