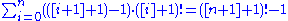Mixed radix
Encyclopedia
Mixed radix numeral system
s are non-standard positional numeral systems
in which the numerical base
varies from position to position. Such numerical representation applies when a quantity is expressed using a sequence of units that are each a multiple of the next smaller one, but not by the same factor. Such units are common for instance in measuring time; a time of 32 weeks, 5 days, 7 hours, 45 minutes, 15 seconds, and 500 milliseconds might be expressed as a number of minutes in mixed-radix notation as:
... 32, 5, 7, 45; 15, 500
... ∞, 7, 24, 60; 60, 1000
or as
In the tabular format, the digits are written above their base, and a semicolon
is used to indicate the radix point
. In numeral format, each digit has its associated base attached as a subscript, and the position of the radix point is indicated by a full stop
. The base for each digit is the number of corresponding units that make up the next larger unit. As a consequence there is no base (written as ∞) for the first (most significant) digit, since here the "next larger unit" does not exist (and note that one could not add a larger unit of "month" or "year" to the sequence of units, as they are not integer multiples of "week").
In this numeral system, the mixed radix numeral 371251251605760 seconds would be interpreted as 05:51:57 p.m. on Wednesday, and 070201202602460 would be 12:02 :24 a.m. on Sunday. Ad hoc notations for mixed radix numeral systems are commonplace.
A second example of a mixed radix numeral system
in current use is in the design and use of currency
, where a limited set of denominations are printed or minted with the objective of being able to represent any monetary quantity; the amount of money is then represented by the number of coins
or banknotes of each denomination. When deciding which denominations to create (and hence which radices to mix), a compromise is aimed for between a minimal number of different denominations, and a minimal number of individual pieces of coinage required to represent typical quantities. So, for example, in the UK, banknotes are printed for £50, £20, £10 and £5, and coins are minted for £2, £1, 50p, 20p, 10p, 5p, 2p and 1p—these follow the 1-2-5 series of preferred values.
In theory, balanced ternary
minimizes the number of pieces of coinage required to represent any quantity.
A historical example of a mixed radix numeral system is the system of Mayan numerals, which generally used base-20, except for the second place (the "10s" in decimal
) which was base-18, so that the first two places counted up to 360 (an approximation to the number of days in the year).
Mixed-radix representation is also relevant to mixed-radix versions of the Cooley-Tukey FFT algorithm
, in which the indices of the input values are expanded in a mixed-radix representation, the indices of the output values are expanded in a corresponding mixed-radix representation with the order of the bases and digits reversed, and each subtransform can be regarded as a Fourier transform in one digit for all values of the remaining digits.
APL
includes operators to convert to and from mixed-radix systems.
number system:
For example, the biggest number that could be represented with six digits would be 543210 which equals 719 in decimal
: 5×5! + 4×4! + 3×3! + 2×2! + 1×1! It might not be clear at first sight but the factorial based numbering system is unambiguous and complete. Every number can be represented in one and only one way because the sum of respective factorials multiplied by the index is always the next factorial minus one:
There is a natural mapping between the integers 0, ..., n! − 1 and permutation
s of n elements in lexicographic order, which uses the factorial representation of the integer, followed by an interpretation as a Lehmer code.
The above equation is a particular case of the following general rule for any radix (either standard or mixed) base representation which expresses the fact that any radix (either standard or mixed) base representation is unambiguous and complete. Every number can be represented in one and only one way because the sum of respective weights multiplied by the index is always the next weight minus one:
which can be easily proved with mathematical induction
.
numbers:
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
s are non-standard positional numeral systems
Non-standard positional numeral systems
Non-standard positional numeral systems here designates numeral systems that may be denoted positional systems, but that deviate in one way or another from the following description of standard positional systems:...
in which the numerical base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
varies from position to position. Such numerical representation applies when a quantity is expressed using a sequence of units that are each a multiple of the next smaller one, but not by the same factor. Such units are common for instance in measuring time; a time of 32 weeks, 5 days, 7 hours, 45 minutes, 15 seconds, and 500 milliseconds might be expressed as a number of minutes in mixed-radix notation as:
... 32, 5, 7, 45; 15, 500
... ∞, 7, 24, 60; 60, 1000
or as
- 32∞577244560.15605001000
In the tabular format, the digits are written above their base, and a semicolon
Semicolon
The semicolon is a punctuation mark with several uses. The Italian printer Aldus Manutius the Elder established the practice of using the semicolon to separate words of opposed meaning and to indicate interdependent statements. "The first printed semicolon was the work of ... Aldus Manutius"...
is used to indicate the radix point
Radix point
In mathematics and computing, a radix point is the symbol used in numerical representations to separate the integer part of a number from its fractional part . "Radix point" is a general term that applies to all number bases...
. In numeral format, each digit has its associated base attached as a subscript, and the position of the radix point is indicated by a full stop
Full stop
A full stop is the punctuation mark commonly placed at the end of sentences. In American English, the term used for this punctuation is period. In the 21st century, it is often also called a dot by young people...
. The base for each digit is the number of corresponding units that make up the next larger unit. As a consequence there is no base (written as ∞) for the first (most significant) digit, since here the "next larger unit" does not exist (and note that one could not add a larger unit of "month" or "year" to the sequence of units, as they are not integer multiples of "week").
Examples
A mixed radix numeral system can often benefit from a tabular summary. The familiar system for describing the 604800 seconds of a week starting from midnight on Sunday runs as follows:| Radix: | 7 | 2 | 12 | 60 | 60 |
| Denomination: | day | half-day | hour | minute | second |
| Place value (seconds): | 86400 | 43200 | 3600 | 60 | 1 |
| Digit translations … | |||||
| day: | 0=Sunday, 1=Monday, 2=Tuesday, 3=Wednesday, 4=Thursday, 5=Friday, 6=Saturday | ||||
| half-day: | 0=AM, 1=PM | ||||
| hour: | 0 is written as "12" (!) | ||||
In this numeral system, the mixed radix numeral 371251251605760 seconds would be interpreted as 05:51:57 p.m. on Wednesday, and 070201202602460 would be 12:02 :24 a.m. on Sunday. Ad hoc notations for mixed radix numeral systems are commonplace.
A second example of a mixed radix numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
in current use is in the design and use of currency
Currency
In economics, currency refers to a generally accepted medium of exchange. These are usually the coins and banknotes of a particular government, which comprise the physical aspects of a nation's money supply...
, where a limited set of denominations are printed or minted with the objective of being able to represent any monetary quantity; the amount of money is then represented by the number of coins
COinS
ContextObjects in Spans, commonly abbreviated COinS, is a method to embed bibliographic metadata in the HTML code of web pages. This allows bibliographic software to publish machine-readable bibliographic items and client reference management software to retrieve bibliographic metadata. The...
or banknotes of each denomination. When deciding which denominations to create (and hence which radices to mix), a compromise is aimed for between a minimal number of different denominations, and a minimal number of individual pieces of coinage required to represent typical quantities. So, for example, in the UK, banknotes are printed for £50, £20, £10 and £5, and coins are minted for £2, £1, 50p, 20p, 10p, 5p, 2p and 1p—these follow the 1-2-5 series of preferred values.
In theory, balanced ternary
Balanced ternary
Balanced ternary is a non-standard positional numeral system , useful for comparison logic. It is a ternary system, but unlike the standard ternary system, the digits have the values −1, 0, and 1...
minimizes the number of pieces of coinage required to represent any quantity.
A historical example of a mixed radix numeral system is the system of Mayan numerals, which generally used base-20, except for the second place (the "10s" in decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
) which was base-18, so that the first two places counted up to 360 (an approximation to the number of days in the year).
Mixed-radix representation is also relevant to mixed-radix versions of the Cooley-Tukey FFT algorithm
Cooley-Tukey FFT algorithm
The Cooley–Tukey algorithm, named after J.W. Cooley and John Tukey, is the most common fast Fourier transform algorithm. It re-expresses the discrete Fourier transform of an arbitrary composite size N = N1N2 in terms of smaller DFTs of sizes N1 and N2, recursively, in order to reduce the...
, in which the indices of the input values are expanded in a mixed-radix representation, the indices of the output values are expanded in a corresponding mixed-radix representation with the order of the bases and digits reversed, and each subtransform can be regarded as a Fourier transform in one digit for all values of the remaining digits.
Manipulation
Mixed-radix numbers of the same base can be manipulated using a generalization of manual arithmetic algorithms. Conversion of values from one mixed base to another is easily accomplished by first converting the place values of the one system into the other, and then applying the digits from the one system against these.APL
APL programming language
APL is an interactive array-oriented language and integrated development environment, which is available from a number of commercial and noncommercial vendors and for most computer platforms. It is based on a mathematical notation developed by Kenneth E...
includes operators to convert to and from mixed-radix systems.
Factorial number system
Another proposal is the so-called factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
number system:
| Radix | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Place value | 7! | 6! | 5! | 4! | 3! | 2! | 1! | 0! |
| Place value in decimal | 5040 | 720 | 120 | 24 | 6 | 2 | 1 | 0 |
| Highest digit allowed | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
For example, the biggest number that could be represented with six digits would be 543210 which equals 719 in decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
: 5×5! + 4×4! + 3×3! + 2×2! + 1×1! It might not be clear at first sight but the factorial based numbering system is unambiguous and complete. Every number can be represented in one and only one way because the sum of respective factorials multiplied by the index is always the next factorial minus one:
There is a natural mapping between the integers 0, ..., n! − 1 and permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of n elements in lexicographic order, which uses the factorial representation of the integer, followed by an interpretation as a Lehmer code.
The above equation is a particular case of the following general rule for any radix (either standard or mixed) base representation which expresses the fact that any radix (either standard or mixed) base representation is unambiguous and complete. Every number can be represented in one and only one way because the sum of respective weights multiplied by the index is always the next weight minus one:
-
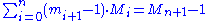 , where
, where 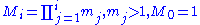 ,
,
which can be easily proved with mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
Prime radix number system
Another interesting proposal is the number system with successive prime numbers as radix, whose place values are primorialPrimorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
numbers:
| radix: | 17 | 13 | 11 | 7 | 5 | 3 | 2 |
| place value: | (p6=13)# | (p5=11)# | (p4=7)# | (p3=5)# | (p2=3)# | (p1=2)# | (p0=1)# |
| decimal: | 30030 | 2310 | 210 | 30 | 6 | 2 | 1 |
-
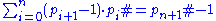 where
where  , and pj = jth prime, p0# = p0 = 1.
, and pj = jth prime, p0# = p0 = 1.