
Autoregressive integrated moving average
Encyclopedia
In statistics
and econometrics
, and in particular in time series analysis, an autoregressive integrated moving average (ARIMA) model is a generalization of an autoregressive moving average (ARMA) model. These models are fitted to time series
data either to better understand the data or to predict future points in the series (forecasting). They are applied in some cases where data show evidence of non-stationarity, where an initial differencing step (corresponding to the "integrated" part of the model) can be applied to remove the non-stationarity.
The model is generally referred to as an ARIMA(p,d,q) model where p, d, and q are non-negative integers that refer to the order of the autoregressive, integrated, and moving average parts of the model respectively. ARIMA models form an important part of the Box-Jenkins
approach to time-series modelling.
When one of the terms is zero, it's usual to drop AR, I or MA. For example, an I(1) model is ARIMA(0,1,0), and a MA(1) model is ARIMA(0,0,1).
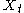 where
where  is an integer index and the
is an integer index and the 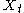 are real numbers, then an ARMA
are real numbers, then an ARMA
(p,q) model is given by:
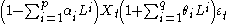
where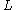 is the lag operator, the
is the lag operator, the 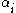 are the parameters of the autoregressive part of the model, the
are the parameters of the autoregressive part of the model, the 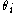 are the parameters of the moving average part and the
are the parameters of the moving average part and the 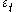 are error terms. The error terms
are error terms. The error terms 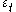 are generally assumed to be independent, identically distributed variables sampled from a normal distribution with zero mean.
are generally assumed to be independent, identically distributed variables sampled from a normal distribution with zero mean.
Assume now that the polynomial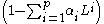 has a unitary root of multiplicity d. Then it can be rewritten as:
has a unitary root of multiplicity d. Then it can be rewritten as:
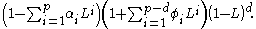
An ARIMA(p,d,q) process expresses this polynomial factorisation property, and is given by:
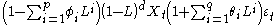
and thus can be thought as a particular case of an ARMA(p+d,q) process having the auto-regressive polynomial with some roots in the unity. For this reason every ARIMA model with d>0 is not wide sense stationary.
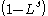 in a model is one way of including a non-stationary seasonality of period s into the model. Another example is the factor
in a model is one way of including a non-stationary seasonality of period s into the model. Another example is the factor 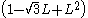 , which includes a (non-stationary) seasonality of period 12. The effect of the first type of factor is to allow each season's value to drift separately over time, whereas with the second type values for adjacent seasons move together.
, which includes a (non-stationary) seasonality of period 12. The effect of the first type of factor is to allow each season's value to drift separately over time, whereas with the second type values for adjacent seasons move together.
Identification and specification of appropriate factors in an ARIMA model can be an important step in modelling as it can allow a reduction in the overeall number of parameters to be estimated, while allowing the imposition on the model of types of behaviour that logic and experience suggest should be there.
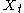 that have some clearly identifiable trends:
that have some clearly identifiable trends:
In these cases the ARIMA model can be viewed as a "cascade" of two models. The first is non-stationary:
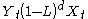
while the second is wide-sense stationary:
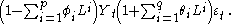
Now standard forecasts techniques can be formulated for the process , and then (having the sufficient number of initial conditions)
, and then (having the sufficient number of initial conditions) 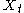 can be forecast via opportune integration steps.
can be forecast via opportune integration steps.
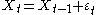
which is simply a random walk
.
A number of variations on the ARIMA model are commonly used. For example, if multiple time series are used then the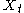 can be thought of as vectors and a VARIMA model may be appropriate. Sometimes a seasonal effect is suspected in the model. For example, consider a model of daily road traffic volumes. Weekends clearly exhibit different behaviour from weekdays. In this case it is often considered better to use a SARIMA (seasonal ARIMA) model than to increase the order of the AR or MA parts of the model. If the time-series is suspected to exhibit long-range dependence then the
can be thought of as vectors and a VARIMA model may be appropriate. Sometimes a seasonal effect is suspected in the model. For example, consider a model of daily road traffic volumes. Weekends clearly exhibit different behaviour from weekdays. In this case it is often considered better to use a SARIMA (seasonal ARIMA) model than to increase the order of the AR or MA parts of the model. If the time-series is suspected to exhibit long-range dependence then the 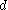 parameter may be replaced by certain non-integer values in an autoregressive fractionally integrated moving average
parameter may be replaced by certain non-integer values in an autoregressive fractionally integrated moving average
model, which is also called a Fractional ARIMA (FARIMA or ARFIMA) model.
parameter optimization are available to find the right parameters for the ARIMA model.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
, and in particular in time series analysis, an autoregressive integrated moving average (ARIMA) model is a generalization of an autoregressive moving average (ARMA) model. These models are fitted to time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
data either to better understand the data or to predict future points in the series (forecasting). They are applied in some cases where data show evidence of non-stationarity, where an initial differencing step (corresponding to the "integrated" part of the model) can be applied to remove the non-stationarity.
The model is generally referred to as an ARIMA(p,d,q) model where p, d, and q are non-negative integers that refer to the order of the autoregressive, integrated, and moving average parts of the model respectively. ARIMA models form an important part of the Box-Jenkins
Box-Jenkins
In time series analysis, the Box–Jenkins methodology, named after the statisticians George Box and Gwilym Jenkins, applies autoregressive moving average ARMA or ARIMA models to find the best fit of a time series to past values of this time series, in order to make forecasts.-Modeling approach:The...
approach to time-series modelling.
When one of the terms is zero, it's usual to drop AR, I or MA. For example, an I(1) model is ARIMA(0,1,0), and a MA(1) model is ARIMA(0,0,1).
Definition
Given a time series of data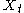 where
where  is an integer index and the
is an integer index and the 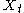 are real numbers, then an ARMA
are real numbers, then an ARMAArma
-Businesses, institutions and organizations:* Agung Rai Museum of Art located in Ubud, Bali - also related to the ARMA resort* American Rock Mechanics Association, a geoscience organization...
(p,q) model is given by:
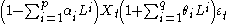
where
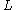 is the lag operator, the
is the lag operator, the 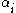 are the parameters of the autoregressive part of the model, the
are the parameters of the autoregressive part of the model, the 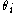 are the parameters of the moving average part and the
are the parameters of the moving average part and the 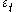 are error terms. The error terms
are error terms. The error terms 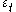 are generally assumed to be independent, identically distributed variables sampled from a normal distribution with zero mean.
are generally assumed to be independent, identically distributed variables sampled from a normal distribution with zero mean.Assume now that the polynomial
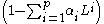 has a unitary root of multiplicity d. Then it can be rewritten as:
has a unitary root of multiplicity d. Then it can be rewritten as: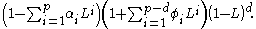
An ARIMA(p,d,q) process expresses this polynomial factorisation property, and is given by:
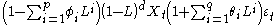
and thus can be thought as a particular case of an ARMA(p+d,q) process having the auto-regressive polynomial with some roots in the unity. For this reason every ARIMA model with d>0 is not wide sense stationary.
Other special forms
The explicit identification of the factorisation of the autoregression polynomial into factors as above, can be extended to other cases, firstly to apply to the moving average polynomial and secondly to include other special factors. For example, having a factor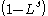 in a model is one way of including a non-stationary seasonality of period s into the model. Another example is the factor
in a model is one way of including a non-stationary seasonality of period s into the model. Another example is the factor 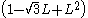 , which includes a (non-stationary) seasonality of period 12. The effect of the first type of factor is to allow each season's value to drift separately over time, whereas with the second type values for adjacent seasons move together.
, which includes a (non-stationary) seasonality of period 12. The effect of the first type of factor is to allow each season's value to drift separately over time, whereas with the second type values for adjacent seasons move together.Identification and specification of appropriate factors in an ARIMA model can be an important step in modelling as it can allow a reduction in the overeall number of parameters to be estimated, while allowing the imposition on the model of types of behaviour that logic and experience suggest should be there.
Forecasts using ARIMA models
ARIMA models are used for observable non-stationary processes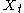 that have some clearly identifiable trends:
that have some clearly identifiable trends:- a constant trend (i.e. zero average) is modeled by
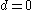
- a linear trend (i.e. linear growth behavior) is modeled by
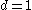
- a quadratic trend (i.e. quadratic growth behavior) is modeled by
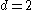
In these cases the ARIMA model can be viewed as a "cascade" of two models. The first is non-stationary:
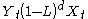
while the second is wide-sense stationary:
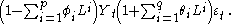
Now standard forecasts techniques can be formulated for the process
 , and then (having the sufficient number of initial conditions)
, and then (having the sufficient number of initial conditions) 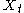 can be forecast via opportune integration steps.
can be forecast via opportune integration steps.Examples
Some well-known special cases arise naturally. For example, an ARIMA(0,1,0) model is given by: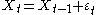
which is simply a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
.
A number of variations on the ARIMA model are commonly used. For example, if multiple time series are used then the
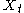 can be thought of as vectors and a VARIMA model may be appropriate. Sometimes a seasonal effect is suspected in the model. For example, consider a model of daily road traffic volumes. Weekends clearly exhibit different behaviour from weekdays. In this case it is often considered better to use a SARIMA (seasonal ARIMA) model than to increase the order of the AR or MA parts of the model. If the time-series is suspected to exhibit long-range dependence then the
can be thought of as vectors and a VARIMA model may be appropriate. Sometimes a seasonal effect is suspected in the model. For example, consider a model of daily road traffic volumes. Weekends clearly exhibit different behaviour from weekdays. In this case it is often considered better to use a SARIMA (seasonal ARIMA) model than to increase the order of the AR or MA parts of the model. If the time-series is suspected to exhibit long-range dependence then the 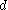 parameter may be replaced by certain non-integer values in an autoregressive fractionally integrated moving average
parameter may be replaced by certain non-integer values in an autoregressive fractionally integrated moving averageAutoregressive fractionally integrated moving average
In statistics, autoregressive fractionally integrated moving average models are time series models that generalize ARIMA models by allowing non-integer values of the differencing parameter and are useful in modeling time series with long memory...
model, which is also called a Fractional ARIMA (FARIMA or ARFIMA) model.
Implementations in statistics packages
Various packages that apply methodology like Box-JenkinsBox-Jenkins
In time series analysis, the Box–Jenkins methodology, named after the statisticians George Box and Gwilym Jenkins, applies autoregressive moving average ARMA or ARIMA models to find the best fit of a time series to past values of this time series, in order to make forecasts.-Modeling approach:The...
parameter optimization are available to find the right parameters for the ARIMA model.
- In RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, the stats package includes an arima function. The function is documented in "ARIMA Modelling of Time Series". Besides the ARIMA(p,d,q) part, the function also includes seasonal factors, an intercept term, and exogenous variables (xreg, called "external regressors"). - The "forecast" package in RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
can automatically select an ARIMA model for a given time series with the auto.arima function. The package can also simulate seasonal and non-seasonal ARIMA models with its simulate.Arima function. It also has a function Arima, which is a wrapper for the arima from the "stats" package. - SAS(R) of "SAS Institute Inc." includes extensive ARIMA processing in its Econometric and Time Series Analysis system: SAS/ETS.
See also
- AutocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
- ARMAAutoregressive moving average modelIn statistics and signal processing, autoregressive–moving-average models, sometimes called Box–Jenkins models after the iterative Box–Jenkins methodology usually used to estimate them, are typically applied to autocorrelated time series data.Given a time series of data Xt, the ARMA model is a...
- X-12-ARIMAX-12-ARIMAX-12-ARIMA is the U.S. Census Bureau's software package for seasonal adjustment. It can be used together with gretl, which provides a graphical user interface for X-12-ARIMA.X-12-ARIMA is the successor to X-11-ARIMA-See also:*AnSWR*ARIMA*CSPro...
- Partial autocorrelation

