Box-Jenkins
Encyclopedia
In time series analysis, the Box–Jenkins methodology
, named after the statistician
s George Box and Gwilym Jenkins
, applies autoregressive moving average ARMA or ARIMA
models to find the best fit of a time series to past values of this time series, in order to make forecast
s.
The data they used were from a gas furnace. These data are well-known as the Box and Jenkins gas furnace data for benchmarking predictive models.
is stationary
and if there is any significant seasonality
that needs to be modeled.
. It can also be detected from an autocorrelation plot. Specifically, non-stationarity is often indicated by an autocorrelation plot with very slow decay.
, or a spectral plot.
and subtracting the fitted values from the original data can also be used in the context of Box–Jenkins models.
estimation software. However, it may be helpful to apply a seasonal difference to the data and regenerate the autocorrelation and partial autocorrelation plots. This may help in the model identification of the non-seasonal component of the model. In some cases, the seasonal differencing may remove most or all of the seasonality effect.
For higher-order autoregressive processes, the sample autocorrelation needs to be supplemented with a partial autocorrelation plot. The partial autocorrelation of an AR(p) process becomes zero at lag p + 1 and greater, so we examine the sample partial autocorrelation function to see if there is evidence of a departure from zero. This is usually determined by placing a 95% confidence interval
on the sample partial autocorrelation plot (most software programs that generate sample autocorrelation plots will also plot this confidence interval). If the software program does not generate the confidence band, it is approximately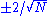
, with N denoting the sample size.
process becomes zero at lag q + 1 and greater, so we examine the sample autocorrelation function to see where it essentially becomes zero. We do this by placing the 95% confidence interval for the sample autocorrelation function on the sample autocorrelation plot. Most software that can generate the autocorrelation plot can also generate this confidence interval.
The sample partial autocorrelation function is generally not helpful for identifying the order of the moving average process.
s and will not give the same picture as the theoretical functions. This makes the model identification more difficult. In particular, mixed models can be particularly difficult to identify.
Although experience is helpful, developing good models using these sample plots can involve much trial and error. For this reason, in recent years information-based criteria such as FPE (final prediction error) and AIC (Akaike Information Criterion
) and others have been preferred and used. These techniques can help automate the model identification process. These techniques require computer software to use. Fortunately, these techniques are available in many commercial statistical software programs that provide ARIMA modeling capabilities.
For additional information on these techniques, see Brockwell and Davis (1987, 2002).
The main approaches to fitting Box–Jenkins models are non-linear least squares and maximum likelihood estimation. Maximum likelihood estimation is generally the preferred technique. The likelihood equations for the full Box–Jenkins model are complicated and are not included here. See (Brockwell and Davis, 1987,2002) for the mathematical details.
That is, the error term At is assumed to follow the assumptions for a stationary univariate process. The residuals should be white noise
(or independent when their distributions are normal) drawings from a fixed distribution with a constant mean and variance. If the Box–Jenkins model is a good model for the data, the residuals should satisfy these assumptions.
If these assumptions are not satisfied, one needs to fit a more appropriate model. That is, go back to the model identification step and try to develop a better model. Hopefully the analysis of the residuals can provide some clues as to a more appropriate model.
One way to assess if the residuals from the Box–Jenkins model follow the assumptions is to generate statistical graphics
(including an autocorrelation plot) of the residuals. One could also look at the value of the Box–Ljung statistic
.
Methodology
Methodology is generally a guideline for solving a problem, with specificcomponents such as phases, tasks, methods, techniques and tools . It can be defined also as follows:...
, named after the statistician
Statistician
A statistician is someone who works with theoretical or applied statistics. The profession exists in both the private and public sectors. The core of that work is to measure, interpret, and describe the world and human activity patterns within it...
s George Box and Gwilym Jenkins
Gwilym Jenkins
Gwilym Meirion Jenkins was a Welsh statistician and systems engineer, born in Gowerton , Swansea, Wales. He is most notable for his pioneering work with George Box on autoregressive moving average models, also called Box-Jenkins models, in time-series analysis.He earned a first class honors degree...
, applies autoregressive moving average ARMA or ARIMA
Autoregressive integrated moving average
In statistics and econometrics, and in particular in time series analysis, an autoregressive integrated moving average model is a generalization of an autoregressive moving average model. These models are fitted to time series data either to better understand the data or to predict future points...
models to find the best fit of a time series to past values of this time series, in order to make forecast
Forecasting
Forecasting is the process of making statements about events whose actual outcomes have not yet been observed. A commonplace example might be estimation for some variable of interest at some specified future date. Prediction is a similar, but more general term...
s.
Modeling approach
The original model uses an iterative three-stage modeling approach:- Model identification and model selectionModel selectionModel selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
: making sure that the variables are stationaryStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, identifying seasonality in the dependent series (seasonally differencing it if necessary), and using plots of the autocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
and partial autocorrelation functions of the dependent time series to decide which (if any) autoregressive or moving average component should be used in the model. - Parameter estimation using computation algorithms to arrive at coefficients which best fit the selected ARIMA model. The most common methods use maximum likelihood estimation or non-linear least-squares estimation.
- Model checkingStatistical model validationIn statistics, model validation is possibly the most important step in the model building sequence. It is also one of the most overlooked. Often the validation of a model seems to consist of nothing more than quoting the R2 statistic from the fit .-R2 is not...
by testing whether the estimated model conforms to the specifications of a stationary univariate process. In particular, the residuals should be independent of each other and constant in mean and variance over time. (Plotting the mean and variance of residuals over time and performing a Ljung-Box testLjung-Box testThe Ljung–Box test is a type of statistical test of whether any of a group of autocorrelations of a time series are different from zero...
or plotting autocorrelation and partial autocorrelation of the residuals are helpful to identify misspecification.) If the estimation is inadequate, we have to return to step one and attempt to build a better model.
The data they used were from a gas furnace. These data are well-known as the Box and Jenkins gas furnace data for benchmarking predictive models.
Stationarity and seasonality
The first step in developing a Box–Jenkins model is to determine if the time seriesTime series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
is stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
and if there is any significant seasonality
Seasonality
In statistics, many time series exhibit cyclic variation known as seasonality, periodic variation, or periodic fluctuations. This variation can be either regular or semi regular....
that needs to be modeled.
Detecting stationarity
Stationarity can be assessed from a run sequence plot. The run sequence plot should show constant location and scaleScale (ratio)
The scale ratio of some sort of model which represents an original proportionally is the ratio of a linear dimension of the model to the same dimension of the original. Examples include a 3-dimensional scale model of a building or the scale drawings of the elevations or plans of a building. In such...
. It can also be detected from an autocorrelation plot. Specifically, non-stationarity is often indicated by an autocorrelation plot with very slow decay.
Detecting seasonality
Seasonality (or periodicity) can usually be assessed from an autocorrelation plot, a seasonal subseries plotSeasonal subseries plot
Seasonal subseries plots are a tool for detecting seasonality in a time series. This plot allows one to detect both between-group and within-group patterns. This plot is only useful if the period of the seasonality is already known. In many cases, this will in fact be known. For example, monthly...
, or a spectral plot.
Differencing to achieve stationarity
Box and Jenkins recommend the differencing approach to achieve stationarity. However, fitting a curveCurve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
and subtracting the fitted values from the original data can also be used in the context of Box–Jenkins models.
Seasonal differencing
At the model identification stage, the goal is to detect seasonality, if it exists, and to identify the order for the seasonal autoregressive and seasonal moving average terms. For many series, the period is known and a single seasonality term is sufficient. For example, for monthly data one would typically include either a seasonal AR 12 term or a seasonal MA 12 term. For Box–Jenkins models, one does not explicitly remove seasonality before fitting the model. Instead, one includes the order of the seasonal terms in the model specification to the ARIMAArima
The Royal Borough of Arima is the fourth largest town in Trinidad and Tobago. Located east of the capital, Port of Spain, Arima supports the only organised indigenous community in the country, the Santa Rosa Carib Community and is the seat of the Carib Queen...
estimation software. However, it may be helpful to apply a seasonal difference to the data and regenerate the autocorrelation and partial autocorrelation plots. This may help in the model identification of the non-seasonal component of the model. In some cases, the seasonal differencing may remove most or all of the seasonality effect.
Identify p and q
Once stationarity and seasonality have been addressed, the next step is to identify the order (i.e., the p and q) of the autoregressive and moving average terms.Autocorrelation and partial autocorrelation plots
The primary tools for doing this are the autocorrelation plot and the partial autocorrelation plot. The sample autocorrelation plot and the sample partial autocorrelation plot are compared to the theoretical behavior of these plots when the order is known.Order of autoregressive process (p)
Specifically, for an AR(1) process, the sample autocorrelation function should have an exponentially decreasing appearance. However, higher-order AR processes are often a mixture of exponentially decreasing and damped sinusoidal components.For higher-order autoregressive processes, the sample autocorrelation needs to be supplemented with a partial autocorrelation plot. The partial autocorrelation of an AR(p) process becomes zero at lag p + 1 and greater, so we examine the sample partial autocorrelation function to see if there is evidence of a departure from zero. This is usually determined by placing a 95% confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
on the sample partial autocorrelation plot (most software programs that generate sample autocorrelation plots will also plot this confidence interval). If the software program does not generate the confidence band, it is approximately
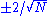, with N denoting the sample size.Order of moving-average process (q)
The autocorrelation function of a MA(q)Moving average model
In time series analysis, the moving-average model is a common approach for modeling univariate time series models. The notation MA refers to the moving average model of order q:...
process becomes zero at lag q + 1 and greater, so we examine the sample autocorrelation function to see where it essentially becomes zero. We do this by placing the 95% confidence interval for the sample autocorrelation function on the sample autocorrelation plot. Most software that can generate the autocorrelation plot can also generate this confidence interval.
The sample partial autocorrelation function is generally not helpful for identifying the order of the moving average process.
Shape of autocorrelation function
The following table summarizes how one can use the sample autocorrelation function for model identification.| Shape | Indicated Model |
|---|---|
| Exponential, decaying to zero | Autoregressive model Autoregressive model In statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena... . Use the partial autocorrelation plot to identify the order of the autoregressive model. |
| Alternating positive and negative, decaying to zero | Autoregressive model. Use the partial autocorrelation plot to help identify the order. |
| One or more spikes, rest are essentially zero | Moving average model Moving average model In time series analysis, the moving-average model is a common approach for modeling univariate time series models. The notation MA refers to the moving average model of order q:... , order identified by where plot becomes zero. |
| Decay, starting after a few lags | Mixed autoregressive and moving average (ARMA Autoregressive moving average model In statistics and signal processing, autoregressive–moving-average models, sometimes called Box–Jenkins models after the iterative Box–Jenkins methodology usually used to estimate them, are typically applied to autocorrelated time series data.Given a time series of data Xt, the ARMA model is a... ) model. |
| All zero or close to zero | Data are essentially random. |
| High values at fixed intervals | Include seasonal autoregressive term. |
| No decay to zero | Series is not stationary. |
Mixed models difficult to identify
In practice, the sample autocorrelation and partial autocorrelation functions are random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s and will not give the same picture as the theoretical functions. This makes the model identification more difficult. In particular, mixed models can be particularly difficult to identify.
Although experience is helpful, developing good models using these sample plots can involve much trial and error. For this reason, in recent years information-based criteria such as FPE (final prediction error) and AIC (Akaike Information Criterion
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
) and others have been preferred and used. These techniques can help automate the model identification process. These techniques require computer software to use. Fortunately, these techniques are available in many commercial statistical software programs that provide ARIMA modeling capabilities.
For additional information on these techniques, see Brockwell and Davis (1987, 2002).
Box–Jenkins model estimation
Estimating the parameters for the Box–Jenkins models is a quite complicated non-linear estimation problem. For this reason, the parameter estimation should be left to a high quality software program that fits Box–Jenkins models. Fortunately, many statistical software programs now fit Box–Jenkins models.The main approaches to fitting Box–Jenkins models are non-linear least squares and maximum likelihood estimation. Maximum likelihood estimation is generally the preferred technique. The likelihood equations for the full Box–Jenkins model are complicated and are not included here. See (Brockwell and Davis, 1987,2002) for the mathematical details.
Assumptions for a stable univariate process
Model diagnostics for Box–Jenkins models is similar to model validation for non-linear least squares fitting.That is, the error term At is assumed to follow the assumptions for a stationary univariate process. The residuals should be white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
(or independent when their distributions are normal) drawings from a fixed distribution with a constant mean and variance. If the Box–Jenkins model is a good model for the data, the residuals should satisfy these assumptions.
If these assumptions are not satisfied, one needs to fit a more appropriate model. That is, go back to the model identification step and try to develop a better model. Hopefully the analysis of the residuals can provide some clues as to a more appropriate model.
One way to assess if the residuals from the Box–Jenkins model follow the assumptions is to generate statistical graphics
Statistical graphics
Statistical graphics, also known as graphical techniques, are information graphics in the field of statistics used to visualize quantitative data.- Overview :...
(including an autocorrelation plot) of the residuals. One could also look at the value of the Box–Ljung statistic
Ljung-Box test
The Ljung–Box test is a type of statistical test of whether any of a group of autocorrelations of a time series are different from zero...
.
External links
- A First Course on Time Series Analysis - an open source book on time series analysis with SAS (Chapter 7)
- Box–Jenkins models in the Engineering Statistics Handbook of NIST