Atmospheric models
Encyclopedia
Static atmospheric models describe how the ideal gas
properties (namely: pressure, temperature, density, and molecular weight) of an atmosphere change, primarily as a function of altitude
.
For example, the US Standard Atmosphere
is essentially a table of values for air temperature, pressure, and mass density, as a function of altitude above sea level.
Other static atmospheric models may have other outputs, or depend on inputs besides altitude.
, which is to say:
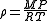
Where ρ is mass density, M is average molecular weight, P is pressure, T is temperature, and R is the ideal gas constant.
The gas is held in place by so called "hydrostatic" forces. That is to say, for a particular layer of gas at some altitude: the downward (towards the planet) force of its weight, the downward force exerted by pressure in the layer above it, and the upward force exerted by pressure in the layer below, all sum to zero. Mathematically this is:
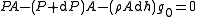
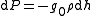
Finally, these variables describing the system do not change with time; i.e. it is a static system.
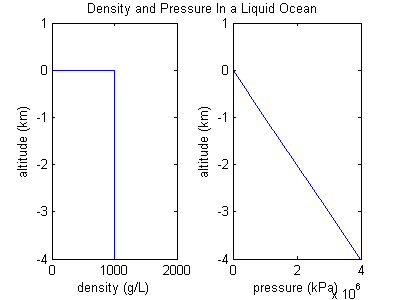
, and this situation looks more like an ocean. Assuming density is constant, then a graph of pressure vs altitude will have a constant slope, since the weight of the ocean above is directly proportional to its depth.
produces the result that density and pressure, the two remaining variables, depend only on each other. For this reason, this model may also be called barotropic
(density depends only on pressure).
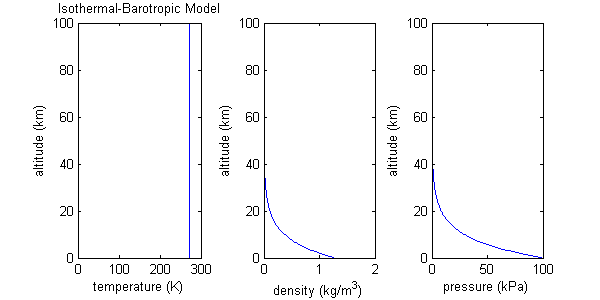
For the isothermal-barotropic model, density and pressure turn out to be exponential functions of altitude. The increase in altitude necessary for P or ρ to drop by 1/e is the called scale height
:
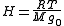
where R is the ideal gas constant, T is temperature, M is average molecular weight, and g0 is the gravitational acceleration at the planet's surface. Using the values T=273 K and M=29 g/mol as characteristic of the Earth's atmosphere, H = RT/Mg = (8.315*273)/(29*9.8) = 7.99, or about 8 km, which coincidentally is approximate height of Mt. Everest.
For an isothermal atmosphere,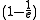
or about 63% of the total mass of the atmosphere exists between the planet's surface and one scale height. (The total air mass below a certain altitude is calculated by integrating over the density function.)
For the ocean example there was a sharp transition in density at the top or "surface" of the ocean. However for atmospheres made of gas there is no equivalent sharp transition or edge. Gas atmospheres simply get less and less dense until they're so thin that they're space.
, decreases with altitude since moving up means moving away from the planet's center.
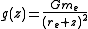
This problem of decreasing g can be dealt with by defining a transformation from real geometric altitude z to an abstraction called "geopotential altitude" h, defined: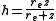
h has the property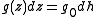
where 
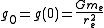
Which basically says the amount of work done lifting a test mass m to height z through an atmosphere where gravity decreases with altitude, is the same as the amount of work done lifting that same mass to a height h through an atmosphere where g magically remains equal to g0, its value at sea level.
This geopotential altitude h is then used instead of geometric altitude z in the hydrostatic equations.
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
properties (namely: pressure, temperature, density, and molecular weight) of an atmosphere change, primarily as a function of altitude
Altitude
Altitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
.
For example, the US Standard Atmosphere
US Standard Atmosphere
The U.S. Standard Atmosphere is a series of models that define values for atmospheric temperature, density, pressure and other properties over a wide range of altitudes. The first model, based on an existing international standard, was published in 1958 by the U.S...
is essentially a table of values for air temperature, pressure, and mass density, as a function of altitude above sea level.
Other static atmospheric models may have other outputs, or depend on inputs besides altitude.
Basic assumptions
The gas which comprises an atmosphere is usually assumed to be an ideal gasIdeal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
, which is to say:
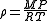
Where ρ is mass density, M is average molecular weight, P is pressure, T is temperature, and R is the ideal gas constant.
The gas is held in place by so called "hydrostatic" forces. That is to say, for a particular layer of gas at some altitude: the downward (towards the planet) force of its weight, the downward force exerted by pressure in the layer above it, and the upward force exerted by pressure in the layer below, all sum to zero. Mathematically this is:
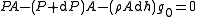
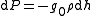
Finally, these variables describing the system do not change with time; i.e. it is a static system.
Some examples
Depending on the model, some gas properties may be treated as constant with respect to altitude.Ocean example
If the density of a gas is constant, then it isn't really behaving like a gas. Instead it is behaving like an incompressible fluid, or liquidLiquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
, and this situation looks more like an ocean. Assuming density is constant, then a graph of pressure vs altitude will have a constant slope, since the weight of the ocean above is directly proportional to its depth.
Isothermal-barotropic approximation and scale height
This atmospheric model assumes both molecular weight and temperature are constant over a wide range of altitude. Such a model may be called isothermal (constant temperature). Inserting constant molecular weight and constant temperature into the equation for the ideal gas lawIdeal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
produces the result that density and pressure, the two remaining variables, depend only on each other. For this reason, this model may also be called barotropic
Barotropic
In meteorology, a barotropic atmosphere is one in which the pressure depends only on the density and vice versa, so that isobaric surfaces are also isopycnic surfaces . The isobaric surfaces will also be isothermal surfaces, hence the geostrophic wind is independent of height...
(density depends only on pressure).
For the isothermal-barotropic model, density and pressure turn out to be exponential functions of altitude. The increase in altitude necessary for P or ρ to drop by 1/e is the called scale height
Scale height
In various scientific contexts, a scale height is a distance over which a quantity decreases by a factor of e...
:
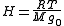
where R is the ideal gas constant, T is temperature, M is average molecular weight, and g0 is the gravitational acceleration at the planet's surface. Using the values T=273 K and M=29 g/mol as characteristic of the Earth's atmosphere, H = RT/Mg = (8.315*273)/(29*9.8) = 7.99, or about 8 km, which coincidentally is approximate height of Mt. Everest.
For an isothermal atmosphere,
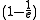or about 63% of the total mass of the atmosphere exists between the planet's surface and one scale height. (The total air mass below a certain altitude is calculated by integrating over the density function.)For the ocean example there was a sharp transition in density at the top or "surface" of the ocean. However for atmospheres made of gas there is no equivalent sharp transition or edge. Gas atmospheres simply get less and less dense until they're so thin that they're space.
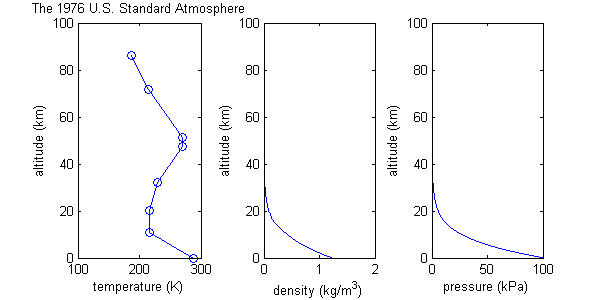
The U.S. Standard Atmosphere
The U.S. Standard Atmosphere model starts with many of the same assumptions as the isothermal-barotropic model, including ideal gas behavior, and constant molecular weight, but it differs by defining a more realistic temperature function, consisting of eight data points connected by straight lines; i.e. regions of constant temperature gradient. (See graph.) Of course the real atmosphere does not have a temperature distribution with this exact shape. The temperature function is an approximation. Values for pressure and density are then calculated based on this temperature function, and the constant temperature gradients help to make some of the math easier.Geopotential altitude
Gravitational acceleration, g(z)Gravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
, decreases with altitude since moving up means moving away from the planet's center.
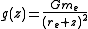
This problem of decreasing g can be dealt with by defining a transformation from real geometric altitude z to an abstraction called "geopotential altitude" h, defined:
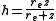
h has the property
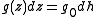where 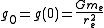Which basically says the amount of work done lifting a test mass m to height z through an atmosphere where gravity decreases with altitude, is the same as the amount of work done lifting that same mass to a height h through an atmosphere where g magically remains equal to g0, its value at sea level.
This geopotential altitude h is then used instead of geometric altitude z in the hydrostatic equations.
Common models
- The US Standard AtmosphereUS Standard AtmosphereThe U.S. Standard Atmosphere is a series of models that define values for atmospheric temperature, density, pressure and other properties over a wide range of altitudes. The first model, based on an existing international standard, was published in 1958 by the U.S...
is one of the most common models - The International Standard AtmosphereInternational Standard AtmosphereThe International Standard Atmosphere is an atmospheric model of how the pressure, temperature, density, and viscosity of the Earth's atmosphere change over a wide range of altitudes. It has been established to provide a common reference for temperature and pressure and consists of tables of...
is a related international standard - NRLMSISE-00NRLMSISE-00NRLMSISE-00 is an empirical, global model of the Earth's atmosphere from ground to space. It models the temperatures and densities of the atmosphere's components. A primary use of this model is to aid predictions of satellite orbital decay due to atmospheric drag...
is a recent model from NRL often used in the atmospheric sciences - The Jacchia Reference AtmosphereJacchia Reference AtmosphereThe Jacchia Reference Atmosphere is an atmospheric model that define values for atmospheric temperature, density, pressure and other properties at altitudes from 90 to 2500 km. Unlike the more common US Standard Atmosphere and related models, the Jacchia model includes latitudinal, seasonal,...
is an older model still commonly used in spacecraft dynamics