
Atiyah algebroid
Encyclopedia
In mathematics
, the Atiyah algebroid, or Atiyah sequence, of a principal G-bundle
P over a manifold M, where G is a Lie group
, is the Lie algebroid
of the gauge groupoid
of P. Explicitly, it is given by the following short exact sequence of vector bundles over M: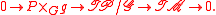
It is named after Michael Atiyah
, who introduced the construction to study the existence theory of complex analytic connections, and it has applications in gauge theory
and mechanics
.
P over a manifold M, with projection π: P→M, the differential
dπ of π defines a short exact sequence
of vector bundles over P, where the vertical bundle
VP is the kernel of the differential projection.
If P is a principal G-bundle, then the group G acts
on the vector bundles in this sequence. The vertical bundle is isomorphic to the trivial g bundle over P, where g is the Lie algebra
of G, and the quotient by the diagonal G action is the associated bundle
P ×G g. The quotient by G of this exact sequence thus yields the Atiyah sequence of vector bundles over M.
of this Lie groupoid
is the Atiyah algebroid.
The space of sections
of the Atiyah algebroid over M is the Lie algebra
of G-invariant vector fields on P under Lie bracket
, which is an extension of the Lie algebra of vector fields on M by the G-invariant vertical vector fields. In an algebraic or analytic context, it is more convenient to view the Atiyah algebroid as an exact sequence of sheaves
of local sections of vector bundles.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Atiyah algebroid, or Atiyah sequence, of a principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
P over a manifold M, where G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, is the Lie algebroid
Lie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
of the gauge groupoid
Lie groupoid
In mathematics, a Lie groupoid is a groupoid where the set Ob of objects and the set Mor of morphisms are both manifolds, the source and target operationss,t : Mor \to Ob...
of P. Explicitly, it is given by the following short exact sequence of vector bundles over M:
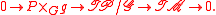
It is named after Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
, who introduced the construction to study the existence theory of complex analytic connections, and it has applications in gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
and mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
.
Direct construction
For any fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
P over a manifold M, with projection π: P→M, the differential
Differential
-Mathematics:* Differential comprises multiple related meanings of the word, both in calculus and differential geometry, such as an infinitesimal change in the value of a function* Differential algebra* Differential calculus...
dπ of π defines a short exact sequence

of vector bundles over P, where the vertical bundle
Vertical bundle
The vertical bundle of a smooth fiber bundle is the subbundle of the tangent bundle that consists of all vectors which are tangent to the fibers...
VP is the kernel of the differential projection.
If P is a principal G-bundle, then the group G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the vector bundles in this sequence. The vertical bundle is isomorphic to the trivial g bundle over P, where g is the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G, and the quotient by the diagonal G action is the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
P ×G g. The quotient by G of this exact sequence thus yields the Atiyah sequence of vector bundles over M.
Lie groupoid viewpoint
Any principal G-bundle P→M has a gauge groupoid, whose objects are points of M, and whose morphisms are elements of the quotient of P×P by the diagonal action of G, with source and target given by the two projections of M. The Lie algebroidLie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
of this Lie groupoid
Lie groupoid
In mathematics, a Lie groupoid is a groupoid where the set Ob of objects and the set Mor of morphisms are both manifolds, the source and target operationss,t : Mor \to Ob...
is the Atiyah algebroid.
The space of sections
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the Atiyah algebroid over M is the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G-invariant vector fields on P under Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
, which is an extension of the Lie algebra of vector fields on M by the G-invariant vertical vector fields. In an algebraic or analytic context, it is more convenient to view the Atiyah algebroid as an exact sequence of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of local sections of vector bundles.

