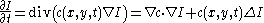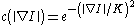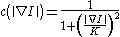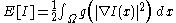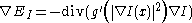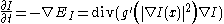Anisotropic diffusion
Encyclopedia
In image processing
and computer vision
, anisotropic diffusion, also called Perona–Malik diffusion, is a technique aiming at reducing image noise without removing significant parts of the image content, typically edges, lines or other details that are important for the interpretation of the image. Anisotropic diffusion resembles the process that creates a scale-space, where an image generates a parameterized family of successively more and more blurred images based on a diffusion process. Each of the resulting images in this family are given as a convolution
between the image and a 2D isotropic Gaussian filter
, where the width of the filter increases with the parameter. This diffusion process is a linear and space-invariant transformation of the original image. Anisotropic diffusion is a generalization of this diffusion process: it produces a family of parameterized images, but each resulting image is a combination between the original image and a filter that depends on the local content of the original image. As a consequence, anisotropic diffusion is a non-linear and space-variant transformation of the original image.
In its original formulation, presented by Perona and Malik
in 1987, the space-variant filter is in fact isotropic but depends on the image content such that it approximates an impulse function close to edges and other structures that should be preserved in the image over the different levels of the resulting scale-space. This formulation was referred to as anisotropic diffusion by Perona and Malik even though the locally adapted filter is isotropic, but it has also been referred to as inhomogeneous and nonlinear diffusion or Perona-Malik diffusion by other authors. A more general formulation allows the locally adapted filter to be truly anisotropic close to linear structures such as edges or lines: it has an orientation given by the structure such that it is elongated along the structure and narrow across. Such methods are referred to as shape-adapted smoothing
or coherence enhancing diffusion. As a consequence, the resulting images preserve linear structures while at the same time smoothing is made along these structures. Both these cases can be described by a generalization of the usual diffusion equation where the diffusion coefficient, instead of being a constant scalar, is a function of image position and assumes a matrix (or tensor) value (see structure tensor
).
Although the resulting family of images can be described as a combination between the original image and space-variant filters, the locally adapted filter and its combination with the image do not have to be realized in practice. Anisotropic diffusion is normally implemented by means of an approximation of the generalized diffusion equation: each new image in the family is computed by applying this equation to the previous image. Consequently, anisotropic diffusion is an iterative process where a relatively simple set of computation are used to compute each successive image in the family and this process is continued until a sufficient degree of smoothing is obtained.
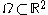 denote a subset of the plane and
denote a subset of the plane and 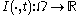 be a family of gray scale images, then anisotropic diffusion is defined as
be a family of gray scale images, then anisotropic diffusion is defined as
where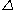 denotes the Laplacian,
denotes the Laplacian, 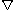 denotes the gradient
denotes the gradient
,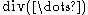 is the divergence
is the divergence
operator and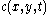 is the diffusion coefficient.
is the diffusion coefficient. 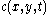 controls the rate of diffusion and is usually chosen as a function of the image gradient so as to preserve edges in the image. Pietro Perona and Jitendra Malik
controls the rate of diffusion and is usually chosen as a function of the image gradient so as to preserve edges in the image. Pietro Perona and Jitendra Malik
pioneered the idea of anisotropic diffusion in 1990 and proposed two functions for the diffusion coefficient:
and
the constant K controls the sensitivity to edges and is usually chosen experimentally or as a function of the noise in the image.
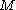 denote the manifold of smooth images, then the diffusion equations presented above can be interpreted as the gradient descent
denote the manifold of smooth images, then the diffusion equations presented above can be interpreted as the gradient descent
equations for the minimization of the energy functional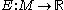 defined by
defined by
where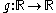 is a real-valued function which we will see is intimately related to the diffusion coefficient. Then for any compactly supported infinitely differentiable test function
is a real-valued function which we will see is intimately related to the diffusion coefficient. Then for any compactly supported infinitely differentiable test function  , we have
, we have
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, anisotropic diffusion, also called Perona–Malik diffusion, is a technique aiming at reducing image noise without removing significant parts of the image content, typically edges, lines or other details that are important for the interpretation of the image. Anisotropic diffusion resembles the process that creates a scale-space, where an image generates a parameterized family of successively more and more blurred images based on a diffusion process. Each of the resulting images in this family are given as a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
between the image and a 2D isotropic Gaussian filter
Gaussian filter
In electronics and signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function. Gaussian filters are designed to give no overshoot to a step function input while minimizing the rise and fall time. This behavior is closely connected to the fact that the Gaussian...
, where the width of the filter increases with the parameter. This diffusion process is a linear and space-invariant transformation of the original image. Anisotropic diffusion is a generalization of this diffusion process: it produces a family of parameterized images, but each resulting image is a combination between the original image and a filter that depends on the local content of the original image. As a consequence, anisotropic diffusion is a non-linear and space-variant transformation of the original image.
In its original formulation, presented by Perona and Malik
Jitendra Malik
Jitendra Malik is a researcher in computer vision, the Arthur J. Chick Professor of Electrical Engineering and Computer Science at the University of California, Berkeley....
in 1987, the space-variant filter is in fact isotropic but depends on the image content such that it approximates an impulse function close to edges and other structures that should be preserved in the image over the different levels of the resulting scale-space. This formulation was referred to as anisotropic diffusion by Perona and Malik even though the locally adapted filter is isotropic, but it has also been referred to as inhomogeneous and nonlinear diffusion or Perona-Malik diffusion by other authors. A more general formulation allows the locally adapted filter to be truly anisotropic close to linear structures such as edges or lines: it has an orientation given by the structure such that it is elongated along the structure and narrow across. Such methods are referred to as shape-adapted smoothing
Affine shape adaptation
Affine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point...
or coherence enhancing diffusion. As a consequence, the resulting images preserve linear structures while at the same time smoothing is made along these structures. Both these cases can be described by a generalization of the usual diffusion equation where the diffusion coefficient, instead of being a constant scalar, is a function of image position and assumes a matrix (or tensor) value (see structure tensor
Structure tensor
In mathematics, the structure tensor, also referred to as the second-moment matrix, is a matrix derived from the gradient of a function. It summarizes the predominant directions of the gradient in a specified neighborhood of a point, and the degree to which those directions are coherent...
).
Although the resulting family of images can be described as a combination between the original image and space-variant filters, the locally adapted filter and its combination with the image do not have to be realized in practice. Anisotropic diffusion is normally implemented by means of an approximation of the generalized diffusion equation: each new image in the family is computed by applying this equation to the previous image. Consequently, anisotropic diffusion is an iterative process where a relatively simple set of computation are used to compute each successive image in the family and this process is continued until a sufficient degree of smoothing is obtained.
Formal definition
Formally, let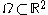 denote a subset of the plane and
denote a subset of the plane and 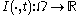 be a family of gray scale images, then anisotropic diffusion is defined as
be a family of gray scale images, then anisotropic diffusion is defined as
where
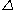 denotes the Laplacian,
denotes the Laplacian, 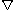 denotes the gradient
denotes the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
,
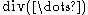 is the divergence
is the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
operator and
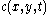 is the diffusion coefficient.
is the diffusion coefficient. 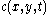 controls the rate of diffusion and is usually chosen as a function of the image gradient so as to preserve edges in the image. Pietro Perona and Jitendra Malik
controls the rate of diffusion and is usually chosen as a function of the image gradient so as to preserve edges in the image. Pietro Perona and Jitendra MalikJitendra Malik
Jitendra Malik is a researcher in computer vision, the Arthur J. Chick Professor of Electrical Engineering and Computer Science at the University of California, Berkeley....
pioneered the idea of anisotropic diffusion in 1990 and proposed two functions for the diffusion coefficient:
and
the constant K controls the sensitivity to edges and is usually chosen experimentally or as a function of the noise in the image.
Motivation
Let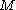 denote the manifold of smooth images, then the diffusion equations presented above can be interpreted as the gradient descent
denote the manifold of smooth images, then the diffusion equations presented above can be interpreted as the gradient descentGradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
equations for the minimization of the energy functional
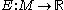 defined by
defined by
where
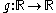 is a real-valued function which we will see is intimately related to the diffusion coefficient. Then for any compactly supported infinitely differentiable test function
is a real-valued function which we will see is intimately related to the diffusion coefficient. Then for any compactly supported infinitely differentiable test function  , we have
, we have-
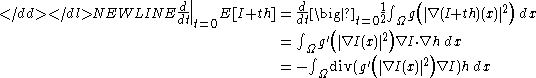
where the last line follow from multidimensional integration by parts. Letting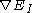 denote the gradient of E with respect to the
denote the gradient of E with respect to the 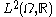 inner product evaluated at I, this gives
inner product evaluated at I, this gives
Therefore, the gradient descentGradient descentGradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
equations on the functional E are given by
Thus by letting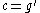 we obtain the anisotropic diffusion equations.
we obtain the anisotropic diffusion equations.
Applications
Anisotropic diffusion can be used to remove noise from digital images without blurring edges. With a constant diffusion coefficient, the anisotropic diffusion equations reduce to the heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
which is equivalent to Gaussian blurring. This is ideal for removing noise but also indiscriminately blurs edges too. When the diffusion coefficient is chosen as an edge seeking function, such as in Perona and Malik, the resulting equations encourage diffusion (hence smoothing) within regions and prohibit it across strong edges. Hence the edges can be preserved while removing noise from the image.
Along the same lines as noise removal, anisotropic diffusion can be used in edge detection algorithms. By running the diffusion with an edge seeking diffusion coefficient for a certain number of iterations, the image can be evolved towards a piecewise constant image with the boundaries between the constant components being detected as edges.
See also
- Bilateral filterBilateral filterA bilateral filter is an edge-preserving and noise reducing smoothing filter. The intensity value at each pixel in an image is replaced by a weighted average of intensity values from nearby pixels. This weight is based on a Gaussian distribution. Crucially the weights depend not only on Euclidean...
- Edge detectionEdge detectionEdge detection is a fundamental tool in image processing and computer vision, particularly in the areas of feature detection and feature extraction, which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities...
- Edge-preserving smoothingEdge-preserving smoothingEdge-preserving smoothing is an image processing technique that smooths away textures whilst retaining sharp edges.1. Usage:When we need to preserve edge information and at the same time preserve the edges. Even when uniform smoothing does not remove the boundaries, it does distort them. This is...
- Heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
- Image noiseImage noiseImage noise is random variation of brightness or color information in images, and is usually an aspect of electronic noise. It can be produced by the sensor and circuitry of a scanner or digital camera...
- Noise reductionNoise reductionNoise reduction is the process of removing noise from a signal.All recording devices, both analogue or digital, have traits which make them susceptible to noise...
- Scale spaceScale spaceScale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision...
- Total variation denoisingTotal variation denoisingIn signal processing, Total variation denoising, also known as total variation regularization is a process, most often used in digital image processing that has applications in noise removal. It is based on the principle that signals with excessive and possibly spurious detail have high total...
External links
- Mathematica PeronaMalikFilter function.
- IDL nonlinear anisotropic diffusion package(edge enhancing and coherence enhancing): http://www2.warwick.ac.uk/fac/sci/physics/research/cfsa/people/yuan/studytracking/computation/idllib/
-