
Amenable Banach algebra
Encyclopedia
A Banach algebra
, A, is amenable if all bounded derivation
s from A into dual Banach A-bimodules are inner (that is of the form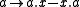 for some
for some  in the dual module).
in the dual module).
An equivalent characterization is that A is amenable if and only if it has a virtual diagonal.
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
, A, is amenable if all bounded derivation
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
s from A into dual Banach A-bimodules are inner (that is of the form
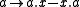 for some
for some  in the dual module).
in the dual module).An equivalent characterization is that A is amenable if and only if it has a virtual diagonal.
Examples
- If A is a group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
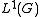 for some locally compact groupLocally compact groupIn mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
for some locally compact groupLocally compact groupIn mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
G then A is amenable if and only if G is amenableAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
. - If A is a C*-algebra then A is amenable if and only if it is nuclear.
- If A is a uniform algebraUniform algebraA uniform algebra A on a compact Hausdorff topological space X is a closed subalgebra of the C*-algebra C with the following properties:As a closed subalgebra of the commutative Banach algebra C a uniform algebra is itself a unital commutative Banach algebra A uniform algebra A on a compact...
on a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
then A is amenable if and only if it is trivial (i.e. the algebra C(X) of all continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on X). - If A is amenable and there is a continuous algebra homomorphism
 from A to another Banach algebra, then the closure of
from A to another Banach algebra, then the closure of 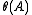 is amenable.
is amenable.

