Alternating direction implicit method
Encyclopedia
In numerical analysis
, the Alternating Direction Implicit (ADI) method is a finite difference
method for solving parabolic
and elliptic partial differential equations. It is most notably used to solve the problem of heat conduction
or solving the diffusion equation in two or more dimensions. It is an example of an operator splitting method.
The traditional method for solving the heat conduction equation numerically is the Crank–Nicolson method. This method results in a very complicated set of equations in multiple dimensions, which are costly to solve. The advantage of the ADI method is that the equations that have to be solved in each step have a simpler structure and can be solved efficiently with the tridiagonal matrix algorithm
.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Alternating Direction Implicit (ADI) method is a finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
method for solving parabolic
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
and elliptic partial differential equations. It is most notably used to solve the problem of heat conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
or solving the diffusion equation in two or more dimensions. It is an example of an operator splitting method.
The traditional method for solving the heat conduction equation numerically is the Crank–Nicolson method. This method results in a very complicated set of equations in multiple dimensions, which are costly to solve. The advantage of the ADI method is that the equations that have to be solved in each step have a simpler structure and can be solved efficiently with the tridiagonal matrix algorithm
Tridiagonal matrix algorithm
In numerical linear algebra, the tridiagonal matrix algorithm , also known as the Thomas algorithm , is a simplified form of Gaussian elimination that can be used to solve tridiagonal systems of equations...
.
The method
Consider the linear diffusion equation in two dimensions,-
The implicit Crank–Nicolson method produces the following finite difference equation:
-
where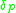
is the central difference operator for the p-coordinate. After performing a stability analysisVon Neumann stability analysisIn numerical analysis, von Neumann stability analysis is a procedure used to check the stability of finite difference schemes as applied to linear partial differential equations...
, it can be shown that this method will be stable for any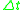
.
A disadvantage of the Crank–Nicolson method is that the matrix in the above equation is bandedBand matrixIn mathematics, particularly matrix theory, a band matrix is a sparse matrix whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.-Matrix bandwidth:...
with a band width that is generally quite large. This makes direct solution of the system of linear equations quite costly (although efficient approximate solutions exist, for example use of the conjugate gradient methodConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
preconditioned with incomplete Cholesky factorizationIncomplete Cholesky factorizationIn numerical analysis, an incomplete Cholesky factorization of a symmetric positive definite matrix is a sparse approximation of the Cholesky factorization...
).
The idea behind the ADI method is to split the finite difference equations into two, one with the x-derivative taken implicitly and the next with the y-derivative taken implicitly,
-
-
The system of equations involved is symmetric and tridiagonal (banded with bandwidth 3), and is typically solved using tridiagonal matrix algorithmTridiagonal matrix algorithmIn numerical linear algebra, the tridiagonal matrix algorithm , also known as the Thomas algorithm , is a simplified form of Gaussian elimination that can be used to solve tridiagonal systems of equations...
.
It can be shown that this method is unconditionally stable and second order in time and space. There are more refined ADI methods such as the methods of Douglas, or the f-factor method which can be used for three or more dimensions.
External links
-
-
-