Alignments of random points, as shown by statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, can be found when a large number of random

Randomness

Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....

 points are marked on a bounded flat surface. This might be used to show that ley line

Ley line

Ley lines are alleged alignments of a number of places of geographical and historical interest, such as ancient monuments and megaliths, natural ridge-tops and water-fords...

s exist due to chance alone (as opposed to supernatural or anthropological explanations).

One precise definition which expresses the generally accepted meaning of "alignment" as:

A set of points, chosen from a given set of landmark points, all of which lie within at least one straight path of a given width w

"Straight path of width w" may be defined as the set of all points within a distance of w/2 of a straight line on a plane, or a great circle

Great circle

A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...

 on a sphere, or in general any geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

 on any other kind of manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

. Note that, in general, any given set of points that are aligned in this way will contain a large number of infinitesimally different straight paths. Therefore, only the existence of at least one straight path is necessary to determine whether a set of points is an alignment. For this reason, it is easier to count the sets of points, rather than the paths themselves.

The width w is important: it allows the fact that real-world features are not mathematical points, and that their positions need not line up exactly for them to be considered in alignment. Alfred Watkins

Alfred Watkins

Alfred Watkins was a businessman, self-taught amateur archaeologist and antiquarian who, while standing on a hillside in Herefordshire, England, in 1921 experienced a revelation and noticed on the British landscape the apparent arrangement of straight lines positioned along ancient features, and...

, in his classic work on ley lines The Old Straight Track

The Old Straight Track

The Old Straight Track: Its Mounds, Beacons, Moats, Sites and Mark Stones is a book by Alfred Watkins, first published in 1925, describing the existence of alleged ley lines in Britain....

, used width of a pencil line on a map as the threshold for the tolerance of what might be regarded as an alignment. For example, using a 1 mm pencil line to draw alignments on an 1:50,000 Ordnance Survey

Ordnance Survey

Ordnance Survey , an executive agency and non-ministerial government department of the Government of the United Kingdom, is the national mapping agency for Great Britain, producing maps of Great Britain , and one of the world's largest producers of maps.The name reflects its creation together with...

 map, a suitable value of w would be 50 m.

An estimate of the probability of alignments existing by chance

Statistically, finding alignments on a landscape gets progressively easier as the geographic area to be considered increases. One way of understanding this phenomenon is to see that the increase in the number of possible combination

Combination

In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...

s of sets of points in that area overwhelms the decrease in the probability that any given set of points in that area line up.

The number of alignments found is very sensitive to the allowed width w, increasing approximately proportionately to w^k-2, where k is the number of points in an alignment.

For those interested in the mathematics, the following is a very approximate order-of-magnitude estimate of the likelihood of alignments, assuming a plane covered with uniformly distributed "significant" points.

Consider a set of n points in a compact area with approximate diameter d and area approximately d². Consider a valid line to be one where every point is within distance w/2 of the line (that is, lies on a track of width w, where w << d).

Consider all the unordered sets of k points from the n points, of which there are:


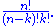
What is the probability that any given set of points is collinear

Collinearity

A set of points is collinear if they lie on a single line. Related concepts include:In mathematics:...

 in this way? Let us very roughly consider the line between the "leftmost" and "rightmost" two points of the k selected points (for some arbitrary left/right axis: we can choose top and bottom for the exceptional vertical case). These two points are by definition on this line. For each of the remaining k-2 points, the probability that the point is "near enough" to the line is roughly w/d, which can be seen by considering the ratio of the area of the line tolerance zone (roughly wd) and the overall area (roughly d²).

So, the expected number of k-point alignments, by this definition, is very roughly:


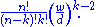
For n >> k this is approximately:


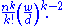
Now assume that area is equal to , and say there is a density α of points such that .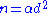

Then we have the expected number of lines equal to:


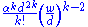
and an area density of k-point lines of:


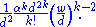
Gathering the terms in k we have an areal density of k-point lines of:


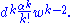
Thus, contrary to intuition, the number of k-point lines expected from random chance increases much more than linearly with the size of the area considered.

A more precise estimate of the expected number of alignments

A more precise expression for the number of 3-point alignments of maximum width w and maximum length d expected by chance among n points placed randomly on a square of side L is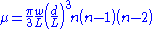

If edge effects (alignments lost over the boundaries of the square) are included, then the expression becomes

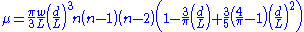
A generalisation to k-point alignments (ignoring edge effects) is

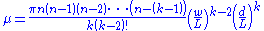
Computer simulation of alignments

Computer simulation

Computer simulation

A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...

s show that points on a plane tend to form alignments similar to those found by ley hunters in numbers consistent with the order-of-magnitude estimates above, suggesting that ley lines may also be generated by chance. This phenomenon occurs regardless of whether the points are generated pseudo-randomly by computer, or from data sets of mundane features such as pizza restaurants.

It is easy to find alignments of 4 to 8 points in reasonably small data sets with w = 50 m.
Choosing large areas or larger values of w makes it easy to find alignments of 20 or more points.