
Affine manifold
Encyclopedia
In differential geometry, an affine manifold is a manifold
equipped with a flat, torsion-free
connection
.
Equivalently, it is a manifold that is (if connected) covered
by an open subset of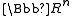 , with monodromy acting by affine transformation
, with monodromy acting by affine transformation
s. This equivalence is an easy corollary of Cartan-Ambrose-Hicks theorem.
Equivalently, it is a manifold equipped with an atlas—called the affine structure—with all transition functions between chart
s affine (that is, have constant jacobian matrix); two atlases are equivalent if the manifold admits an atlas subjugated to both, with transitions from both atlases to a smaller atlas being affine. A manifold having a distinguished affine structure is called an affine manifold and the charts which are affinely related to those of the affine structure are called affine charts. In each affine coordinate domain the coordinate vector field
s form a parallelization of that domain, so there is an associated connection on each domain. These locally defined connections are the same on overlapping parts, so there is a unique connection associated with an affine structure.
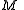 is a real manifold
is a real manifold
with charts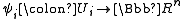 such that
such that 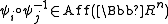 for all
for all 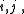 where
where 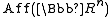 denotes the Lie group
denotes the Lie group
of affine transformations.
An affine manifold is called complete if its universal covering is isomorphic to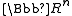 .
.
A fundamental group of a compact complete flat affine manifold is called an affine crystallographic group. Classification of affine crystallographic groups is a difficult problem, far from being solved. The Riemannian crystallographic groups
(also known as Bieberbach groups) were classified by L. Bieberbach, answering a question posed by Hilbert. In his work on Hilbert's 18-th problem
, Bieberbach proved that any Riemannian crystallographic group contains an abelian subgroup of finite index.
The most important of them are
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
equipped with a flat, torsion-free
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
.
Equivalently, it is a manifold that is (if connected) covered
Covering
-Mathematics:*In topology:** Covering map, a function from one space to another with uniform local neighborhoods** Cover , a system of sets whose union is a given topological space...
by an open subset of
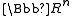 , with monodromy acting by affine transformation
, with monodromy acting by affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s. This equivalence is an easy corollary of Cartan-Ambrose-Hicks theorem.
Equivalently, it is a manifold equipped with an atlas—called the affine structure—with all transition functions between chart
Chart
A chart is a graphical representation of data, in which "the data is represented by symbols, such as bars in a bar chart, lines in a line chart, or slices in a pie chart"...
s affine (that is, have constant jacobian matrix); two atlases are equivalent if the manifold admits an atlas subjugated to both, with transitions from both atlases to a smaller atlas being affine. A manifold having a distinguished affine structure is called an affine manifold and the charts which are affinely related to those of the affine structure are called affine charts. In each affine coordinate domain the coordinate vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s form a parallelization of that domain, so there is an associated connection on each domain. These locally defined connections are the same on overlapping parts, so there is a unique connection associated with an affine structure.
Formal definition
An affine manifold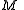 is a real manifold
is a real manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with charts
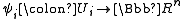 such that
such that 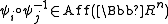 for all
for all 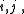 where
where 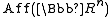 denotes the Lie group
denotes the Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of affine transformations.
An affine manifold is called complete if its universal covering is isomorphic to
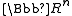 .
.A fundamental group of a compact complete flat affine manifold is called an affine crystallographic group. Classification of affine crystallographic groups is a difficult problem, far from being solved. The Riemannian crystallographic groups
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
(also known as Bieberbach groups) were classified by L. Bieberbach, answering a question posed by Hilbert. In his work on Hilbert's 18-th problem
Hilbert's eighteenth problem
Hilbert's eighteenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by mathematician David Hilbert. It asks three separate questions about lattices and sphere packing in Euclidean space....
, Bieberbach proved that any Riemannian crystallographic group contains an abelian subgroup of finite index.
Important longstanding conjectures
Geometry of affine manifolds is essentially a network of longstanding conjectures; most of them proven in low dimension and some other special cases.The most important of them are
- Markus conjecture (1961) stating that a compact affine manifold is complete if and only if it has constant volume. Known in dimension 3.
- Auslander conjecture (1964) stating that any affine crystallographic group contains a polycyclic subgroupPolycyclic groupIn mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
of finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
. Known in dimensions up to 6, and when the holonomy of the flat connection preserves a Lorentz metric. Since every virtually polycyclic crystallographic group preserves a volume form, Auslander conjecture implies the "only if" part of the Markus conjecture.
- Chern conjecture (1955) The Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of an affine manifold vanishes.

