Hardy-Littlewood circle method
Encyclopedia
In mathematics
, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory
. It is named for G. H. Hardy
and J. E. Littlewood, who developed it in a series of papers on Waring's problem
.
a few years earlier, in 1916 and 1917, on the asymptotics of the partition function
. It was taken up by many other researchers, including Harold Davenport
and I. M. Vinogradov, who modified the formulation slightly (moving from complex analysis
to exponential sum
s), without changing the broad lines. Hundreds of papers followed, and the method still yields results. The method is the subject of a monograph by R. C. Vaughan.
of the series, then computing the residues about zero (essentially the Fourier coefficients). Technically, the generating function is scaled to have radius of convergence 1, so it has singularities on the unit circle – thus one cannot take the contour integral over the unit circle.
The circle method is specifically how to compute these residues, by partitioning
the circle into minor arcs (the bulk of the circle) and major arcs (small arcs containing the most significant singularities), and then bounding the behavior on the minor arcs. The key insight is that, in many cases of interest (such as theta functions), the singularities occur at the roots of unity, and the significance of the singularities is in the order of the Farey sequence
. Thus one can investigate the most significant singularities, and, if fortunate, compute the integrals.
in the complex plane. Assuming the problem had first been formulated in the terms that for a sequence of complex numbers
we want some asymptotic information of the type
where we have some heuristic
reason to guess the form taken by F (an ansatz
), we write
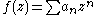
a power series generating function
. The interesting cases are where f is then of radius of convergence
equal to 1, and we suppose that the problem as posed has been modified to present this situation.
that
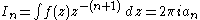
for integers n ≥ 0, where the integral is taken over the circle of radius r and centred at 0, for any r with
That is, this is a contour integral, with the contour being the circle described traversed once anti-clockwise. So far, this is relatively elementary. We would like to take r = 1 directly, i.e. to use the unit circle contour. In the complex analysis formulation this is problematic, since the values of f are not in general defined there.
of rational numbers, or equivalently by the roots of unity
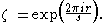
Here the denominator s, assuming that r/s is in lowest terms, turns out to determine the relative importance of the singular behaviour of typical f near ζ.
, smaller in order than F(n).
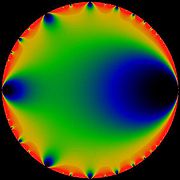It is the case, as the false-colour diagram indicates, that for a theta function the 'most important' point on the boundary circle is at z = 1; followed by z = −1, and then the two complex cube roots of unity at 7 o'clock and 11 o'clock. After that it is the fourth roots of unity i and −i that matter most. While nothing in this guarantees that the analytical method will work, it does explain the rationale of using a Farey series-type criterion on roots of unity.
In the Waring problem case, one takes a sufficiently high power of the generating function, to force the situation in which the singularities, organised into the so-called singular series, do predominate. The less wasteful the estimates used on the rest, the finer the results. As Bryan Birch has put it, the method is inherently wasteful. That does not apply to the partition function case, which signalled the possibility that in a favourable situation the losses from estimates could be controlled.
so that the relevant integral In is a Fourier coefficient. Vinogradov applied finite sums to Waring's problem
in 1926, and the general trigometric sum method became known as "the circle method of Hardy, Littlewood and Ramanujan, in the form of Vinogradov's trigonometric sums"; found on pp. 387–8 of K. K. Mardzhanishvili (1985). Essentially all this does is to discard the whole 'tail' of the generating function, allowing the business of r in the limiting operation to be set directly to the value 1.
s, as long as the number of variables k is large relative to the degree d (see Birch's theorem
for example). This turns out to be a contribution to the Hasse principle
, capable of yielding quantitative information. If d is fixed and k is small, other methods are required, and indeed the Hasse principle tends to fail.
found a modification of the contour that makes the series arising from the circle method converge to the exact result. To describe his contour, it is convenient to replace the unit circle by the upper half plane, by making the substitution z = exp(2πiτ), so that the contour integral becomes an integral from τ = i to τ = 1 + i. (The number i could be replaced by any number on the upper half plane, but i is the most convenient choice.) Rademacher's contour is (more or less) given by the boundaries of all the Ford circle
s from 0 to 1, as shown in the diagram. The replacement of the line from i to 1 + i by the boundaries of these circles is a non-trivial limiting process, which can be justified for modular forms that have negative weight, and with more care can also be justified for non-constant terms for the case of weight 0 (in other words modular functions).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
. It is named for G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and J. E. Littlewood, who developed it in a series of papers on Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
.
History
The initial germ of the idea is usually attributed to the work of Hardy with Srinivasa RamanujanSrinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
a few years earlier, in 1916 and 1917, on the asymptotics of the partition function
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
. It was taken up by many other researchers, including Harold Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
and I. M. Vinogradov, who modified the formulation slightly (moving from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
to exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
s), without changing the broad lines. Hundreds of papers followed, and the method still yields results. The method is the subject of a monograph by R. C. Vaughan.
Outline
The goal is to prove asymptotic behavior of a series: to show that an ~ F(n) for some function. This is done by taking the generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the series, then computing the residues about zero (essentially the Fourier coefficients). Technically, the generating function is scaled to have radius of convergence 1, so it has singularities on the unit circle – thus one cannot take the contour integral over the unit circle.
The circle method is specifically how to compute these residues, by partitioning
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
the circle into minor arcs (the bulk of the circle) and major arcs (small arcs containing the most significant singularities), and then bounding the behavior on the minor arcs. The key insight is that, in many cases of interest (such as theta functions), the singularities occur at the roots of unity, and the significance of the singularities is in the order of the Farey sequence
Farey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
. Thus one can investigate the most significant singularities, and, if fortunate, compute the integrals.
Setup
The circle in question was initially the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex plane. Assuming the problem had first been formulated in the terms that for a sequence of complex numbers
- an, n = 0, 1, 2, 3, ...
we want some asymptotic information of the type
- an ~ F(n)
where we have some heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
reason to guess the form taken by F (an ansatz
Ansatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
), we write
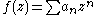
a power series generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
. The interesting cases are where f is then of radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
equal to 1, and we suppose that the problem as posed has been modified to present this situation.
Residues
From that formulation, it is direct from the residue theoremResidue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
that
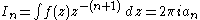
for integers n ≥ 0, where the integral is taken over the circle of radius r and centred at 0, for any r with
- 0 < r < 1.
That is, this is a contour integral, with the contour being the circle described traversed once anti-clockwise. So far, this is relatively elementary. We would like to take r = 1 directly, i.e. to use the unit circle contour. In the complex analysis formulation this is problematic, since the values of f are not in general defined there.
Singularities on unit circle
The problem addressed by the circle method is to force the issue of taking r = 1, by a good understanding of the nature of the singularities f exhibits on the unit circle. The fundamental insight is the role played by the Farey sequenceFarey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
of rational numbers, or equivalently by the roots of unity
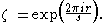
Here the denominator s, assuming that r/s is in lowest terms, turns out to determine the relative importance of the singular behaviour of typical f near ζ.
Method
The Hardy–Littlewood circle method, for the complex-analytic formulation, can then be thus expressed. The contributions to the evaluation of In, as r → 1, should be treated in two ways, traditionally called major arcs and minor arcs. We divide the ζ into two classes, according to whether s ≤ N, or s > N, where N is a function of n that is ours to choose conveniently. The integral In is divided up into integrals each on some arc of the circle that is adjacent to ζ, of length a function of s (again, at our discretion). The arcs make up the whole circle; the sum of the integrals over the major arcs is to make up 2πiF(n) (realistically, this will happen up to a manageable remainder term). The sum of the integrals over the minor arcs is to be replaced by an upper boundUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
, smaller in order than F(n).
Discussion
Stated baldly like this, it is not at all clear that this can be made to work. Indeed, the insights involved are not so shallow. One clear source is the theory of theta functions.Waring's problem
In the context of Waring's problem, powers of theta functions are the generating functions for sums of squares. Their analytic behaviour is known in much more accurate detail than for the cubes, for example.In the Waring problem case, one takes a sufficiently high power of the generating function, to force the situation in which the singularities, organised into the so-called singular series, do predominate. The less wasteful the estimates used on the rest, the finer the results. As Bryan Birch has put it, the method is inherently wasteful. That does not apply to the partition function case, which signalled the possibility that in a favourable situation the losses from estimates could be controlled.
Vinogradov trigonometric sums
Later, I. M. Vinogradov extended the technique, replacing the exponential sum formulation f(z) with a finite Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
so that the relevant integral In is a Fourier coefficient. Vinogradov applied finite sums to Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
in 1926, and the general trigometric sum method became known as "the circle method of Hardy, Littlewood and Ramanujan, in the form of Vinogradov's trigonometric sums"; found on pp. 387–8 of K. K. Mardzhanishvili (1985). Essentially all this does is to discard the whole 'tail' of the generating function, allowing the business of r in the limiting operation to be set directly to the value 1.
Applications
Refinements of the method have allowed results to be proved about the solutions of homogeneous Diophantine equationDiophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s, as long as the number of variables k is large relative to the degree d (see Birch's theorem
Birch's theorem
In mathematics, Birch's theorem, named for Bryan John Birch, is a statement about the representability of zero by odd degree forms.-Statement of Birch's theorem:...
for example). This turns out to be a contribution to the Hasse principle
Hasse principle
In mathematics, Helmut Hasse's local-global principle, also known as the Hasse principle, is the idea that one can find an integer solution to an equation by using the Chinese remainder theorem to piece together solutions modulo powers of each different prime number...
, capable of yielding quantitative information. If d is fixed and k is small, other methods are required, and indeed the Hasse principle tends to fail.
Rademacher's contour
In the special case when the circle method is applied to find the coefficients of a modular form of negative weight, Hans RademacherHans Rademacher
Hans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
found a modification of the contour that makes the series arising from the circle method converge to the exact result. To describe his contour, it is convenient to replace the unit circle by the upper half plane, by making the substitution z = exp(2πiτ), so that the contour integral becomes an integral from τ = i to τ = 1 + i. (The number i could be replaced by any number on the upper half plane, but i is the most convenient choice.) Rademacher's contour is (more or less) given by the boundaries of all the Ford circle
Ford circle
In mathematics, a Ford circle is a circle with centre at and radius 1/, where p/q is an irreducible fraction, i.e. p and q are coprime integers...
s from 0 to 1, as shown in the diagram. The replacement of the line from i to 1 + i by the boundaries of these circles is a non-trivial limiting process, which can be justified for modular forms that have negative weight, and with more care can also be justified for non-constant terms for the case of weight 0 (in other words modular functions).