Abstract rewriting system
Encyclopedia
In mathematical logic
and theoretical computer science
, an abstract rewriting system (also (abstract) reduction system or abstract rewrite system; abbreviation ARS) is a formalism
that captures the quintessential notion and properties of rewriting
systems. In its simplest form, an ARS is simply a set (of "objects") together with a binary relation
, traditionally denoted with
; this definition can be further refined if we index (label) subsets of the binary relation. Despite its simplicity, an ARS is sufficient to describe important properties of rewriting systems like normal forms, termination, and various notions of confluence.
Historically, there have been several formalizations of rewriting in an abstract setting, each with its idiosyncrasies. This is due in part to the fact that some notions are equivalent, as we shall see in this article. The formalization that is most commonly encountered in monographs and textbooks, and which we generally follow here, is due to Gérard Huet
(1980).
An ARS is simply a set A, whose elements are usually called objects, together with a binary relation
on A, traditionally denoted by →, and called the reduction relation, rewrite relation or just reduction. This (entrenched) terminology using "reduction" is a little misleading, because the relation is not necessarily reducing some measure of the objects; this will become more apparent when we discuss string rewriting systems further in this article.
In some contexts it may be beneficial to distinguish between some subsets of the rules, i.e. some subsets of the reduction relation →, e.g. the entire reduction relation may consist of associativity
and commutativity
rules. Consequently, some authors define the reduction relation → as the indexed union of some relations; for instance if
, the notation used is (A, →1, →2).
As a mathematical object, an ARS is exactly the same as unlabeled state transition system
, and if we consider the relation as an indexed union, then an ARS is the same as a labeled state transition system with the indices being the labels. The focus of the study, and the terminology are different however. In a state transition system
one is interested in interpreting the labels as actions, whereas in an ARS the focus is on how objects may be transformed (rewritten) into others.
; otherwise it is called irreducible or a normal form. An object y is called a normal form of x if 
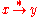, and y is irreducible. If x has a unique normal form, then this is usually denoted with 
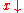. In example 1 above, c is a normal form, and 
. If every object has at least one normal form, the ARS is called normalizing.
One of the important problems that may be formulated in an ARS is the word problem: given x and y are they equivalent under
? This is a very general setting for formulating the word problem for the presentation of an algebraic structure
. For instance, the word problem for groups
is a particular case of an ARS word problem. Central to an "easy" solution for the word problem is the existence of unique normal forms: in this case if two objects have the same normal form, then they are equivalent under
. The word problem for an ARS is undecidable
in general.
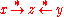. From this definition, it's apparent one may define the joinability relation as 
, where 
is the composition of relations
. Joinability is usually denoted, somewhat confusingly, also with
, but in this notation the down arrow is a binary relation, i.e. we write 
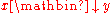if x and y are joinable.
An ARS is said to possess the Church-Rosser property if and only if
implies 
for all objects x, y. Equivalently, the Church-Rosser property means that the reflexive transitive symmetric closure is contained in the joinability relation. Alonzo Church
and J. Barkley Rosser proved in 1936 that lambda calculus
has this property; hence the name of the property. (The fact that lambda calculus has this property is also known as the Church-Rosser theorem.) In an ARS with the Church-Rosser property the word problem may be reduced to the search for a common successor. In a Church-Rosser system, an object has at most one normal form; that is the normal form of an object is unique if it exists, but it may well not exist. In lambda calculus for instance, the expression (λx.xx)(λx.xx) does not have a normal form because there exists an infinite sequence of beta reductions (λx.xx)(λx.xx) → (λx.xx)(λx.xx) → ...
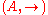is said to be,
Theorem. For an ARS the following three conditions are equivalent: (i) it has the Church-Rosser property, (ii) it is confluent, (iii) it is semi-confluent.
Corollary. In a confluent ARS if
then
Because of these equivalences, a fair bit of variation in definitions is encountered in the literature. For instance, in Terese the Church-Rosser property and confluence are defined to be synonymous and identical to the definition of confluence presented here; Church-Rosser as defined here remains unnamed, but is given as an equivalent property; this departure from other texts is deliberate. Because of the above corollary, one may define a normal form y of x as an irreducible y with the property that
. This definition, found in Book and Otto, is equivalent to common one given here in a confluent system, but it is more inclusive in a non-confluent ARS.
Local confluence on the other hand is not equivalent with the other notions of confluence given in this section, but it is strictly weaker than confluence. The typical counterexample is
, which is locally confluent but not confluent.
. In a terminating ARS, every object has at least one normal form, thus it is normalizing. The converse is not true. In example 1 for instance, there is an infinite rewriting chain, namely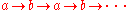 
, even though the system is normalizing. A confluent and terminating ARS is called convergent. In a convergent ARS, every object has a unique normal form. But it is sufficient for the system to be confluent and normalizing for a unique normal to exist for every element, as seen in example 1.
Theorem (Newman's Lemma
): A terminating ARS is confluent if and only if it is locally confluent.
The original 1942 proof of this result by Newman was rather complicated. It wasn't until 1980 that Huet published a much simpler proof exploiting the fact that when
is terminating we can apply well-founded induction.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, an abstract rewriting system (also (abstract) reduction system or abstract rewrite system; abbreviation ARS) is a formalism
Formalism (mathematics)
In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules....
that captures the quintessential notion and properties of rewriting
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
systems. In its simplest form, an ARS is simply a set (of "objects") together with a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
, traditionally denoted with
; this definition can be further refined if we index (label) subsets of the binary relation. Despite its simplicity, an ARS is sufficient to describe important properties of rewriting systems like normal forms, termination, and various notions of confluence.Historically, there have been several formalizations of rewriting in an abstract setting, each with its idiosyncrasies. This is due in part to the fact that some notions are equivalent, as we shall see in this article. The formalization that is most commonly encountered in monographs and textbooks, and which we generally follow here, is due to Gérard Huet
Gérard Huet
Gérard Pierre Huet is a French computer scientist.- Biography :Gérard Huet graduated from the Université Denis Diderot , Case Western Reserve University, and the Université de Paris....
(1980).
Definition
We need to specify a set of objects and the rules that can be applied to transform them. The most general (unidimensional) setting of this notion is called an abstract reduction system, (abbreviated ARS), although more recently authors use abstract rewriting system as well. (The preference for the word "reduction" here instead of "rewriting" constitutes a departure from the uniform use of "rewriting" in the names of systems that are particularizations of ARS. Because the word "reduction" does not appear in the names of more specialized systems, in older texts reduction system is a synonym for ARS).An ARS is simply a set A, whose elements are usually called objects, together with a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on A, traditionally denoted by →, and called the reduction relation, rewrite relation or just reduction. This (entrenched) terminology using "reduction" is a little misleading, because the relation is not necessarily reducing some measure of the objects; this will become more apparent when we discuss string rewriting systems further in this article.
In some contexts it may be beneficial to distinguish between some subsets of the rules, i.e. some subsets of the reduction relation →, e.g. the entire reduction relation may consist of associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
rules. Consequently, some authors define the reduction relation → as the indexed union of some relations; for instance if
, the notation used is (A, →1, →2).As a mathematical object, an ARS is exactly the same as unlabeled state transition system
State transition system
In theoretical computer science, a state transition system is an abstract machine used in the study of computation. The machine consists of a set of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition...
, and if we consider the relation as an indexed union, then an ARS is the same as a labeled state transition system with the indices being the labels. The focus of the study, and the terminology are different however. In a state transition system
State transition system
In theoretical computer science, a state transition system is an abstract machine used in the study of computation. The machine consists of a set of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition...
one is interested in interpreting the labels as actions, whereas in an ARS the focus is on how objects may be transformed (rewritten) into others.
Example 1
Suppose the set of objects is T = {a, b, c} and the binary relation is given by the rules a → b, b → a, a → c, and b → c. Observe that these rules can be applied to both a and b in any fashion to get c. Such a property is clearly an important one. Note also, that c is, in a sense, a "simplest" object in the system, since nothing can be applied to c to transform it any further.Basic notions
Example 1 leads us to define some important notions in the general setting of an ARS. First we need some basic notions and notations.-
is the transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of
, where = is the identity relation, i.e. 
is the smallest preorderPreorderIn mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
(reflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
relation) containing
. It is also called the reflexive transitive closure of 
. -
is 
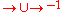, that is the union of the relation → with its inverse relationInverse relationIn mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
, also known as the symmetric closureSymmetric closureIn mathematics, the symmetric closure of a binary relation R on a set X is the smallest symmetric relation on X that contains R....
of
. -
is the transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of
, that is 
is the smallest equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
containing
. It is also known as the reflexive transitive symmetric closure of 
.
Normal forms and the word problem
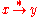An object x in A is called reducible if there exist some other y in A and; otherwise it is called irreducible or a normal form. An object y is called a normal form of x if , and y is irreducible. If x has a unique normal form, then this is usually denoted with 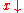. In example 1 above, c is a normal form, and . If every object has at least one normal form, the ARS is called normalizing.One of the important problems that may be formulated in an ARS is the word problem: given x and y are they equivalent under
? This is a very general setting for formulating the word problem for the presentation of an algebraic structureWord problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
. For instance, the word problem for groups
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
is a particular case of an ARS word problem. Central to an "easy" solution for the word problem is the existence of unique normal forms: in this case if two objects have the same normal form, then they are equivalent under
. The word problem for an ARS is undecidableUndecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
in general.
Joinability and the Church–Rosser property
A related, but weaker notion than the existence of normal forms is that of two objects being joinable: x and y are said joinable if the exists some z with the property that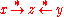. From this definition, it's apparent one may define the joinability relation as , where is the composition of relationsComposition of relations
In mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
. Joinability is usually denoted, somewhat confusingly, also with
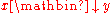, but in this notation the down arrow is a binary relation, i.e. we write if x and y are joinable.An ARS is said to possess the Church-Rosser property if and only if
implies for all objects x, y. Equivalently, the Church-Rosser property means that the reflexive transitive symmetric closure is contained in the joinability relation. Alonzo ChurchAlonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
and J. Barkley Rosser proved in 1936 that lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
has this property; hence the name of the property. (The fact that lambda calculus has this property is also known as the Church-Rosser theorem.) In an ARS with the Church-Rosser property the word problem may be reduced to the search for a common successor. In a Church-Rosser system, an object has at most one normal form; that is the normal form of an object is unique if it exists, but it may well not exist. In lambda calculus for instance, the expression (λx.xx)(λx.xx) does not have a normal form because there exists an infinite sequence of beta reductions (λx.xx)(λx.xx) → (λx.xx)(λx.xx) → ...
Notions of confluence
Various properties, simpler than Church-Rosser, are equivalent to it. The existence of these equivalent properties allows one to prove that a system is Church-Rosser with less work. Furthermore, the notions of confluence can be defined as properties of a particular object, something that's not possible for Church-Rosser. An ARS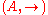 is said to be,- confluent if and only if for all w, x, and y in A,
implies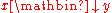 
. Roughly speaking, confluence says that no matter how two paths diverge from a common ancestor (w), the paths are joining at some common successor. This notion may be refined as property of a particular object w, and the system called confluent if all its elements are confluent. - semi-confluent if and only if for all w, x, and y in A,
implies 
. This differs from confluence by the single step reduction from w to x. - locally confluent if and only if for all w, x, and y in A,
implies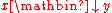 
. This property is sometimes called weak confluence.
Theorem. For an ARS the following three conditions are equivalent: (i) it has the Church-Rosser property, (ii) it is confluent, (iii) it is semi-confluent.
Corollary. In a confluent ARS if
then
- If both x and y are normal forms, then x = y.
- If y is a normal form, then
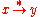
Because of these equivalences, a fair bit of variation in definitions is encountered in the literature. For instance, in Terese the Church-Rosser property and confluence are defined to be synonymous and identical to the definition of confluence presented here; Church-Rosser as defined here remains unnamed, but is given as an equivalent property; this departure from other texts is deliberate. Because of the above corollary, one may define a normal form y of x as an irreducible y with the property that
. This definition, found in Book and Otto, is equivalent to common one given here in a confluent system, but it is more inclusive in a non-confluent ARS.Local confluence on the other hand is not equivalent with the other notions of confluence given in this section, but it is strictly weaker than confluence. The typical counterexample is
, which is locally confluent but not confluent.Termination and convergence
An abstract rewriting system is said to be terminating or noetherian if there is no infinite chain. In a terminating ARS, every object has at least one normal form, thus it is normalizing. The converse is not true. In example 1 for instance, there is an infinite rewriting chain, namely 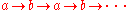, even though the system is normalizing. A confluent and terminating ARS is called convergent. In a convergent ARS, every object has a unique normal form. But it is sufficient for the system to be confluent and normalizing for a unique normal to exist for every element, as seen in example 1.Theorem (Newman's Lemma
Newman's lemma
In the theory of rewriting systems, Newman's lemma states that a terminating abstract rewriting system , that is, one in which there are no infinite reduction sequences, is confluent if it is locally confluent...
): A terminating ARS is confluent if and only if it is locally confluent.
The original 1942 proof of this result by Newman was rather complicated. It wasn't until 1980 that Huet published a much simpler proof exploiting the fact that when
is terminating we can apply well-founded induction.Further reading
A textbook suitable for undergraduates.- Nachum Dershowitz and Jean-Pierre Jouannaud Rewrite Systems, Chapter 6 in Jan van LeeuwenJan van LeeuwenJan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
(Ed.), Handbook of Theoretical Computer Science, Volume B: Formal Models and Sematics., Elsevier and MIT Press, 1990, ISBN 0-444-88074-7, pp.243–320. The preprintPreprintA preprint is a draft of a scientific paper that has not yet been published in a peer-reviewed scientific journal.-Role:Publication of manuscripts in a peer-reviewed journal often takes weeks, months or even years from the time of initial submission, because manuscripts must undergo extensive...
of this chapter is freely available from the authors, but it misses the figures. - Ronald V. BookRonald V. BookRonald Vernon Book worked in theoretical computer science. He published more than 150 papers in scientific journals...
and Friedrich Otto, String-rewriting Systems, Springer (1993). Chapter 1, "Abstract reduction systems" - Marc Bezem, Jan Willem KlopJan Willem KlopJan Willem Klop is a professor of applied logic at Vrije Universiteit in Amsterdam. He holds a Ph.D. in mathematical logic from Utrecht University. Klop is known for his work on the Algebra of Communicating Processes, co-author of TeReSe and his fixed point combinatorwhere- External links :*...
, Roel de Vrijer ("Terese"), Term rewriting systems, Cambridge University Press, 2003, ISBN 0-521-39115-6, Chapter 1. This is a comprehensive monograph. It uses however a fair deal of notations and definitions not commonly encountered elsewhere. For instance the Church–Rosser property is defined to be identical with confluence. - John HarrisonJohn HarrisonJohn Harrison was a self-educated English clockmaker. He invented the marine chronometer, a long-sought device in solving the problem of establishing the East-West position or longitude of a ship at sea, thus revolutionising and extending the possibility of safe long distance sea travel in the Age...
, Handbook of Practical Logic and Automated Reasoning, Cambridge University Press, 2009, ISBN 978-0-521-89957-4, chapter 4 "Equality". Abstract rewriting from the practical perspective of solving problems in equational logic. - Gérard HuetGérard HuetGérard Pierre Huet is a French computer scientist.- Biography :Gérard Huet graduated from the Université Denis Diderot , Case Western Reserve University, and the Université de Paris....
, Confluent Reductions: Abstract Properties and Applications to Term Rewriting Systems, Journal of the ACM (JACM), October 1980, Volume 27, Issue 4, pp. 797–821. Huet's paper established many of the modern concepts, results and notations.