Aberth method
Encyclopedia
The Aberth method, or Aberth–Ehrlich method, named after Oliver Aberth and Louis W. Ehrlich, is a root-finding algorithm
for simultaneous approximation of all the roots of a univariate polynomial
.
The fundamental theorem of algebra
states that for each polynomial with complex coefficients there are as many roots as the degree of the polynomial. More specifically, each polynomial of degree n is identical to a product of n linear polynomials. The fundamental theorem in itself does not offer an efficient numerical procedure to compute those roots. Numerical algorithms that approximate all roots at once are the Weierstrass–(Durand–Kerner) method and the Aberth–Ehrlich method.
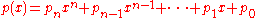be a univariate
polynomial of degree n with real or complex coefficients. Then there exist complex numbers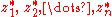
, the roots of p(x), that give the factorisation:
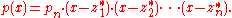
Although those numbers are unknown, upper and lower bounds of their absolute values are computable from the coefficients of the polynomial. Now one can pick n distinct numbers in the complex plane—randomly or evenly distributed—such that their absolute values obey the same bounds. The set of those numbers is called the initial approximation of the set of roots of p(x).This approximation is iteratively improved by the following procedure.
Let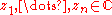
be the current approximations of the zeros of p(x). Then offset numbers 
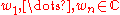are computed as
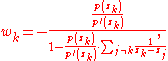
where p'(z) is the polynomial derivative of p evaluated in the point z.
The next set of approximations of roots of p(x) is then
. One can measure the quality of the current approximation by the values of the polynomial or by the size of the offsets.
Inside the formula of the Aberth method one can find elements of Newton's method
and the Weierstrass–(Durand–Kerner) method. Details for an efficient implementation, esp. on the choice of good initial approximations, can be found in Bini (1996).
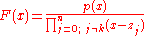
If the values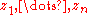
are already close to the roots of p(x), then the rational function F(x) is almost linear with poles at 
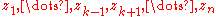that direct the Newton iteration away from the roots of p(x) that are close to them. That is, the corresponding bassins of attraction get rather small.
The Newton step in the univariate case is the reciprocal value to the logarithmic derivative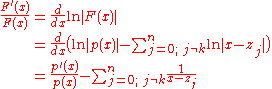
Thus,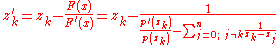
results in the Aberth–Ehrlich iteration.
The iteration may be executed in a simultaneous Jacobi-like iteration where first all new approximations are computed from the old approximations or in a sequential Gauss–Seidel-like iteration that uses each new approximation from the time it is computed.
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
for simultaneous approximation of all the roots of a univariate polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
.
The fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
states that for each polynomial with complex coefficients there are as many roots as the degree of the polynomial. More specifically, each polynomial of degree n is identical to a product of n linear polynomials. The fundamental theorem in itself does not offer an efficient numerical procedure to compute those roots. Numerical algorithms that approximate all roots at once are the Weierstrass–(Durand–Kerner) method and the Aberth–Ehrlich method.
Description
Let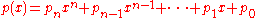 be a univariateUnivariate
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
polynomial of degree n with real or complex coefficients. Then there exist complex numbers
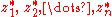, the roots of p(x), that give the factorisation: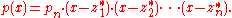Although those numbers are unknown, upper and lower bounds of their absolute values are computable from the coefficients of the polynomial. Now one can pick n distinct numbers in the complex plane—randomly or evenly distributed—such that their absolute values obey the same bounds. The set of those numbers is called the initial approximation of the set of roots of p(x).This approximation is iteratively improved by the following procedure.
Let
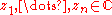be the current approximations of the zeros of p(x). Then offset numbers 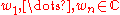are computed as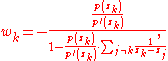where p'(z) is the polynomial derivative of p evaluated in the point z.
The next set of approximations of roots of p(x) is then
. One can measure the quality of the current approximation by the values of the polynomial or by the size of the offsets.Inside the formula of the Aberth method one can find elements of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
and the Weierstrass–(Durand–Kerner) method. Details for an efficient implementation, esp. on the choice of good initial approximations, can be found in Bini (1996).
Derivation from Newton's method
The iteration formula is the univariate Newton iteration for the function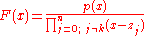If the values
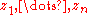are already close to the roots of p(x), then the rational function F(x) is almost linear with poles at 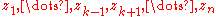that direct the Newton iteration away from the roots of p(x) that are close to them. That is, the corresponding bassins of attraction get rather small.The Newton step in the univariate case is the reciprocal value to the logarithmic derivative
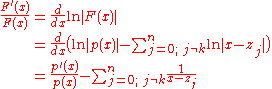
Thus,
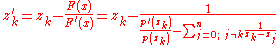
results in the Aberth–Ehrlich iteration.
The iteration may be executed in a simultaneous Jacobi-like iteration where first all new approximations are computed from the old approximations or in a sequential Gauss–Seidel-like iteration that uses each new approximation from the time it is computed.
See also
- MPSolveMPSolveMPSolve is a package for the approximation of the roots of a univariate polynomial. It uses the Aberth method....
A package for numerical computation of polynomial roots. Free usage for scientific purpose.