
Abel's summation formula
Encyclopedia
In mathematics
, Abel's summation formula, introduced by Niels Henrik Abel
, is intensively used in number theory
to compute series
..
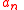 be a sequence
be a sequence
of real
or complex number
s and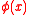 a function
a function
of class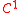 . Then
. Then
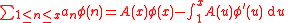
where
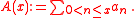
Indeed, this is integration by parts
for a Riemann–Stieltjes integral.
More generally, we have
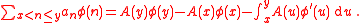
 and
and  then
then  and
and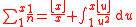
which is a method to represent the Euler–Mascheroni constant
.
 and
and 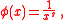 then
then  and
and
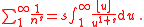
The formula holds for It may be used to derive Dirichlet's theorem, that is,
It may be used to derive Dirichlet's theorem, that is, 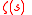 has a simple pole with residue
has a simple pole with residue
1 in s = 1.
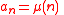 is the Möbius function
is the Möbius function
and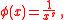 then
then  is Mertens function and
is Mertens function and
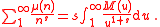
This formula holds for
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Abel's summation formula, introduced by Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
, is intensively used in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
to compute series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
..
Identity
Let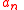 be a sequence
be a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and
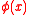 a function
a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of class
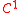 . Then
. Then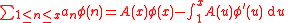
where
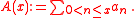
Indeed, this is integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
for a Riemann–Stieltjes integral.
More generally, we have
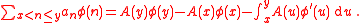
Euler–Mascheroni constant
If and
and  then
then  and
and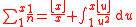
which is a method to represent the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
Representation of Riemann's zeta function
If and
and 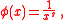 then
then  and
and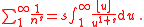
The formula holds for
 It may be used to derive Dirichlet's theorem, that is,
It may be used to derive Dirichlet's theorem, that is, 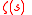 has a simple pole with residue
has a simple pole with residueResidue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
1 in s = 1.
Riemann zeta function
If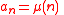 is the Möbius function
is the Möbius functionMöbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
and
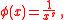 then
then  is Mertens function and
is Mertens function and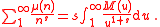
This formula holds for


