Ordinal Ordinal number In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...	Two hundred [and] seventieth
Cardinal Cardinal number In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...	Two hundred [and] seventy
Factorization Factorization In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
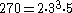Roman numeral	CCLXX
Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...	100001110
Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...	10E

In mathematics

• 270 is a harmonic divisor number
  Harmonic divisor number
  In mathematics, a harmonic divisor number, or Ore number , is a positive integer whose divisors have a harmonic mean that is an integer. The first few harmonic divisor numbers are...
  
  
• 270 is the fourth number that is divisible by its average integer divisor
• 270 is a practical number
  Practical number
  In number theory, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisors of n...
  
  , by the second definition
• The sum of the coprime
  Coprime
  In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
  
   counts for the first 29 integers is 270
• 270 is a sparsely totient number, the largest integer with 72 as its totient
• Given 6 elements, there are 270 square permutations
• 10! has 270 divisor
  Divisor
  In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
  
  s
• 270 is a Harshad number
  Harshad number
  A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
  
   in base 10
• 270 is the smallest positive integer that has divisors ending by digits 1, 2, …, 9.

In other fields

• The year 270 BC
  270 BC
  Year 270 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Clepsina and Blasio...
  
  
• The year 270
  270
  Year 270 was a common year starting on Saturday of the Julian calendar. At the time, it was known as the Year of the Consulship of Antiochianus and Orfitus...
  
   AD
• The caliber of the .270 Winchester
  .270 Winchester
  The .270 Winchester was developed by Winchester Repeating Arms Company in 1923 and unveiled in 1925 as a chambering for their bolt-action Model 54. The cartridge is based upon the .30-06 Springfield...
  
   rifle
• The number of U.S. Electoral College votes needed to be President of the United States
  President of the United States
  The President of the United States of America is the head of state and head of government of the United States. The president leads the executive branch of the federal government and is the commander-in-chief of the United States Armed Forces....
  
  
• The average number of days in human pregnancy
  Pregnancy
  Pregnancy refers to the fertilization and development of one or more offspring, known as a fetus or embryo, in a woman's uterus. In a pregnancy, there can be multiple gestations, as in the case of twins or triplets...
  
  
• A pseudonym for Konami musician Naoki Maeda
• One of a number of secondary Interstate highways connecting to Interstate 70
  Interstate 70
  Interstate 70 is an Interstate Highway in the United States that runs from Interstate 15 near Cove Fort, Utah, to a Park and Ride near Baltimore, Maryland. It was the first Interstate Highway project in the United States. I-70 approximately traces the path of U.S. Route 40 east of the Rocky...
  
  : Interstate 270
  Interstate 270
  Interstate 270 is the designation for several Interstate Highways in the United States, all of which are related to Interstate 70:*Interstate 270 , a connection in Denver*Interstate 270 , a partial beltway around St. Louis...
  
  

271

• Two hundred [and] seventy-one prime, twin prime with 269, cuban prime, centered hexagonal number
  Centered hexagonal number
  A centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice....
  
  , sum of eleven consecutive primes (7 + 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41 + 43).

272

• Two hundred [and] seventy-two 272 = 2⁴·17, sum of four consecutive primes (61 + 67 + 71 + 73), Euler number, primitive semiperfect number
  Primitive semiperfect number
  In number theory, a primitive semiperfect number is a semiperfect number that has no semiperfect proper divisor....
  
  , pronic number
  Pronic number
  A pronic number, oblong number, rectangular number or heteromecic number, is a number which is the product of two consecutive integers, that is, n . The n-th pronic number is twice the n-th triangular number and n more than the n-th square number...
  
  

274

• Two hundred [and] seventy-four = 2·137, tribonacci number, Smith number
  Smith number
  A Smith number is a composite number for which, in a given base , the sum of its digits is equal to the sum of the digits in its prime factorization. For example, 378 = 2 × 3 × 3 × 3 × 7 is a Smith number since 3 + 7 + 8 =...
  
  , nontotient
  Nontotient
  In number theory, a nontotient is a positive integer n which is not in the range of Euler's totient function φ, that is, for which φ = n has no solution. In other words, n is a nontotient if there is no integer x that has exactly n coprimes below it. All odd numbers are nontotients, except 1,...
  
  , noncototient
  Noncototient
  In mathematics, a noncototient is a positive integer n that cannot be expressed as the difference between a positive integer m and the number of coprime integers below it. That is, m − φ = n, where φ stands for Euler's totient function, has no solution for m...
  
  , centered triangular number
  Centered triangular number
  A centered triangular number is a centered figurate number that represents a triangle with a dot in the center and all other dots surrounding the center in successive triangular layers...
  
  

279

• Two hundred [and] seventy-nine 279 = 3²·31 Every positive integer is the sum of at most 279 eighth powers. See Waring's problem
  Waring's problem
  In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...