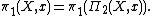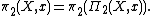2-group
Encyclopedia
In mathematics
, a 2-group, or 2-dimensional higher group, is a certain combination of group
and groupoid
. The 2-groups are part of a larger hierarchy of n-groups. In some of the literature, 2-groups are also called gr-categories or groupal groupoids.
G in which every morphism is invertible and every object has a weak inverse. (Here, a weak inverse of an object x is an object y such that xy and yx are both isomorphic to the unit object.)
A strict 2-group is a group object
in a category of categories; as such, they are also called groupal categories. Conversely, a strict 2-group is a category object in the category of groups
; as such, they are also called categorical groups. They can also be identified with crossed module
s, and are most often studied in that form. Thus, 2-groups in general can be seen as a weakening of crossed modules.
Every 2-group is equivalent to a strict 2-group, although this can't be done coherently: it doesn't extend to 2-group homomorphisms.
on any 2-group G that assigns a weak inverse to each object and makes that object an adjoint equivalance in the monoidal category G.
Given a bicategory
B and an object x of B, there is an automorphism 2-group of x in B, written AutB(x). The objects are the automorphism
s of x, with multiplication given by composition, and the morphisms are the invertible 2-morphisms between these. If B is a 2-groupoid (so all objects and morphisms are weakly invertible) and x is its only object, then AutB(x) is the only data left in B. Thus, 2-groups may be identified with one-object 2-groupoids, much as groups may be idenitified with one-object groupoids and monoidal categories may be identified with one-object bicategories.
If G is a strict 2-group, then the objects of G form a group, called the underlying group of G and written G0. This will not work for arbitrary 2-groups; however, if one identifies isomorphic objects, then the equivalence classes form a group, called the fundamental group of G and written π1(G). (Note that even for a strict 2-group, the fundamental group will only be a quotient group
of the underlying group.)
As a monoidal category, any 2-group G has a unit object IG. The automorphism group of IG is an abelian group
by the Eckmann–Hilton argument, written Aut(IG) or π2(G).
The fundamental group of G act
s on either side of π2(G), and the associator of G (as a monoidal category) defines an element of the cohomology group
H3(π1(G),π2(G)). In fact, 2-groups are classified
in this way: given a group π1, an abelian group π2, a group action of π1 on π2, and an element of H3(π1,π2), there is a unique (up to
equivalence) 2-group G with π1(G) isomorphic to π1, π2(G) isomorphic to π2, and the other data corresponding.
X and a point x in that space, there is a fundamental 2-group of X at x, written Π2(X,x). As a monoidal category, the objects are loop
s at x, with multiplication given by concatenation, and the morphisms are basepoint-preserving homotopies
between loops, with these morphisms identified if they are themselves homotopic.
Conversely, given any 2-group G, one can find a unique (up to
weak homotopy equivalence) pointed
connected space
whose fundamental 2-group is G and whose homotopy group
s πn are trivial for n > 2. In this way, 2-groups classify
pointed connected weak homotopy 2-types. This is a generalisation of the construction of Eilenberg–Mac Lane spaces.
If X is a topological space with basepoint x, then the fundamental group
of X at x is the same as the fundamental group of the fundamental 2-group of X at x; that is,
This fact is the origin of the term "fundamental" in both of its 2-group instances.
Similarly,
Thus, both the first and second homotopy group
s of a space are contained within its fundamental 2-group. As this 2-group also defines an action of π1(X,x) on π2(X,x) and an element of the cohomology group H3(π1(X,x),π2(X,x)), this is precisely the data needed to form the Postnikov tower of X if X is a pointed connected homotopy 2-type.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a 2-group, or 2-dimensional higher group, is a certain combination of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
. The 2-groups are part of a larger hierarchy of n-groups. In some of the literature, 2-groups are also called gr-categories or groupal groupoids.
Definition
A 2-group is a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
G in which every morphism is invertible and every object has a weak inverse. (Here, a weak inverse of an object x is an object y such that xy and yx are both isomorphic to the unit object.)
Strict 2-groups
Much of the literature focuses on strict 2-groups. A strict 2-group is a strict monoidal category in which every morphism is invertible and every object has a strict inverse (so that xy and yx are actually equal to the unit object).A strict 2-group is a group object
Group object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
in a category of categories; as such, they are also called groupal categories. Conversely, a strict 2-group is a category object in the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
; as such, they are also called categorical groups. They can also be identified with crossed module
Crossed module
In mathematics, and especially in homotopy theory, a crossed module consists of groups G and H, where G acts on H , and a homomorphism of groups...
s, and are most often studied in that form. Thus, 2-groups in general can be seen as a weakening of crossed modules.
Every 2-group is equivalent to a strict 2-group, although this can't be done coherently: it doesn't extend to 2-group homomorphisms.
Properties
Weak inverses can always be assigned coherently: one can define a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
on any 2-group G that assigns a weak inverse to each object and makes that object an adjoint equivalance in the monoidal category G.
Given a bicategory
Bicategory
In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...
B and an object x of B, there is an automorphism 2-group of x in B, written AutB(x). The objects are the automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of x, with multiplication given by composition, and the morphisms are the invertible 2-morphisms between these. If B is a 2-groupoid (so all objects and morphisms are weakly invertible) and x is its only object, then AutB(x) is the only data left in B. Thus, 2-groups may be identified with one-object 2-groupoids, much as groups may be idenitified with one-object groupoids and monoidal categories may be identified with one-object bicategories.
If G is a strict 2-group, then the objects of G form a group, called the underlying group of G and written G0. This will not work for arbitrary 2-groups; however, if one identifies isomorphic objects, then the equivalence classes form a group, called the fundamental group of G and written π1(G). (Note that even for a strict 2-group, the fundamental group will only be a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of the underlying group.)
As a monoidal category, any 2-group G has a unit object IG. The automorphism group of IG is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
by the Eckmann–Hilton argument, written Aut(IG) or π2(G).
The fundamental group of G act
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s on either side of π2(G), and the associator of G (as a monoidal category) defines an element of the cohomology group
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
H3(π1(G),π2(G)). In fact, 2-groups are classified
Classification theorem
In mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class....
in this way: given a group π1, an abelian group π2, a group action of π1 on π2, and an element of H3(π1,π2), there is a unique (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
equivalence) 2-group G with π1(G) isomorphic to π1, π2(G) isomorphic to π2, and the other data corresponding.
Fundamental 2-group
Given a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X and a point x in that space, there is a fundamental 2-group of X at x, written Π2(X,x). As a monoidal category, the objects are loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
s at x, with multiplication given by concatenation, and the morphisms are basepoint-preserving homotopies
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between loops, with these morphisms identified if they are themselves homotopic.
Conversely, given any 2-group G, one can find a unique (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
weak homotopy equivalence) pointed
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
connected space
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
whose fundamental 2-group is G and whose homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s πn are trivial for n > 2. In this way, 2-groups classify
Classification theorem
In mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class....
pointed connected weak homotopy 2-types. This is a generalisation of the construction of Eilenberg–Mac Lane spaces.
If X is a topological space with basepoint x, then the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X at x is the same as the fundamental group of the fundamental 2-group of X at x; that is,
This fact is the origin of the term "fundamental" in both of its 2-group instances.
Similarly,
Thus, both the first and second homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of a space are contained within its fundamental 2-group. As this 2-group also defines an action of π1(X,x) on π2(X,x) and an element of the cohomology group H3(π1(X,x),π2(X,x)), this is precisely the data needed to form the Postnikov tower of X if X is a pointed connected homotopy 2-type.
External links
- 2008 Workshop on Categorical Groups at the Centre de Recerca MatemàticaCentre de Recerca MatemàticaThe Centre de Recerca Matemàtica is a consortium, with its own legal status, integrated by the Institut d'Estudis Catalans and the Catalan Government . It is a research institute associated with the Universitat Autònoma de Barcelona...