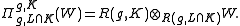Zuckerman functor
Encyclopedia
In mathematics
, a Zuckerman functor is used to construct representations of real reductive
Lie group
s from representations of Levi subgroups. They were introduced by Gregg Zuckerman
(1978). The Bernstein functor is closely related.

and the Bernstein functor Π is defined by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Zuckerman functor is used to construct representations of real reductive
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s from representations of Levi subgroups. They were introduced by Gregg Zuckerman
Gregg Zuckerman
Gregg Jay Zuckerman is a mathematician at Yale University who discovered Zuckerman functors and translation functors, and with Anthony Knapp classified the irreducible tempered representations ofsemisimple Lie groups.-Publications:...
(1978). The Bernstein functor is closely related.
Notation and terminology
- G is a connected reductive real affine algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
(for simplicity; the theory works for more general groups), and g is the Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G. K is a maximal compact subgroupMaximal compact subgroupIn mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of G. - L is a Levi subgroup of G, the centralizer of a compact connected abelian subgroup, and *l is the Lie algebra of L.
- A representation of K is called K-finiteK-finiteIn mathematics, a K-finite function is a type of generalized trigonometric polynomial. Here K is some compact group, and the generalization is from the circle group T....
if every vector is contained in a finite dimensional representation of K. Denote by WK the subspace of K-finite vectors of a representation W of K. - A (g,K)-module is a vector space with compatible actions of g and K, on which the action of K is K-finite.
- R(g,K) is the Hecke algebraHecke algebraIn mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
of G of all distributions on G with support in K that are left and right K finite. This is a ring which does not have an identity but has an approximate identityApproximate identityIn functional analysis and ring theory, an approximate identity is a net in a Banach algebra or ring that acts as a substitute for an identity element....
, and the approximately unital R(g,K)- modules are the same as (g,K) modules.
Definition
The Zuckerman functor Γ is defined by
and the Bernstein functor Π is defined by