
Weyl transformation
Encyclopedia
In theoretical physics
, the Weyl transformation, named after Hermann Weyl
, is a local rescaling of the metric tensor
:
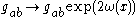
which produces another metric in the same conformal class. A theory or an expression invariant under this transformation is called conformally invariant, or is said to possess Weyl symmetry. The Weyl symmetry is an important symmetry
in conformal field theory
. It is, for example, a symmetry of the Polyakov action
.
The ordinary Levi-Civita connection
and associated spin connection
s are not invariant under Weyl transformations. An appropriately invariant notion is the Weyl connection, which is one way of specifying the structure of a conformal connection
.
A quantity φ has conformal weight k if, under the Weyl transformation, it transforms via
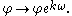
Thus conformally weighted quantities belong to certain density bundles; see also conformal dimension
. Let Aμ be the connection one-form associated to the Levi-Civita connection of g. Introduce a connection that depends also on an initial one-form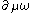 via
via
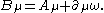
Then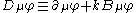 is covariant and has conformal weight
is covariant and has conformal weight  .
.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Weyl transformation, named after Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, is a local rescaling of the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
:
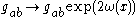
which produces another metric in the same conformal class. A theory or an expression invariant under this transformation is called conformally invariant, or is said to possess Weyl symmetry. The Weyl symmetry is an important symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
. It is, for example, a symmetry of the Polyakov action
Polyakov action
In physics, the Polyakov action is the two-dimensional action of a conformal field theory describing the worldsheet of a string in string theory...
.
The ordinary Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
and associated spin connection
Spin connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the Levi-Civita connection...
s are not invariant under Weyl transformations. An appropriately invariant notion is the Weyl connection, which is one way of specifying the structure of a conformal connection
Conformal connection
In conformal differential geometry, a conformal connection is a Cartan connection on an n-dimensional manifold M arising as a deformation of the Klein geometry given by the celestial n-sphere, viewed as the homogeneous space...
.
A quantity φ has conformal weight k if, under the Weyl transformation, it transforms via
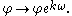
Thus conformally weighted quantities belong to certain density bundles; see also conformal dimension
Conformal dimension
In mathematics, the conformal dimension of a metric space X is the infimum of the Hausdorff dimension over the conformal gauge of X, that is, the class of all metric spaces quasisymmetric to X.-Formal definition:...
. Let Aμ be the connection one-form associated to the Levi-Civita connection of g. Introduce a connection that depends also on an initial one-form
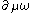 via
via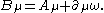
Then
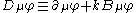 is covariant and has conformal weight
is covariant and has conformal weight  .
.

