Conformal dimension
Encyclopedia
In mathematics, the conformal dimension of a metric space
X is the infimum of the Hausdorff dimension
over the conformal gauge of X, that is, the class of all metric spaces quasisymmetric
to X.
be the collection of all metric spaces that are quasisymmetric to X. The conformal dimension of X is defined as such
, for a metric space X:
The second inequality is true by definition. The first one is deduced from the fact that the topological dimension is invariant by homeomorphism
, and thus can be defined as the infimum
of the Hausdorff dimension
over all spaces homeomorphic to X.
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
X is the infimum of the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
over the conformal gauge of X, that is, the class of all metric spaces quasisymmetric
Quasisymmetric map
In mathematics, a quasisymmetric homeomorphism between metric spaces is a map that generalizes bi-Lipschitz maps. While bi-Lipschitz maps shrink or expand the diameter of a set by no more than a multiplicative factor, quasisymmetric maps satisfy the weaker geometric property that they preserve the...
to X.
Formal definition
Let X be a metric space and be the collection of all metric spaces that are quasisymmetric to X. The conformal dimension of X is defined as such
Properties
We have the following inequalitiesInequality
In mathematics, an inequality is a statement how the relative size or order of two objects, or about whether they are the same or not .*The notation a b means that a is greater than b....
, for a metric space X:
The second inequality is true by definition. The first one is deduced from the fact that the topological dimension is invariant by homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
, and thus can be defined as the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
over all spaces homeomorphic to X.
Examples
- The conformal dimension of
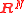is N, since the topological and Hausdorff dimensions of Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s agree.
- The Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
K is of null conformal dimension. However, there is no metric space quasisymmetric to K with a 0 Hausdorff dimension.