
Well-ordering principle
Encyclopedia
The "well-ordering principle" is a property of ordered sets. A set X is well ordered (that is, the set has the well ordering property) if every subset of X has a least element. An example of a well ordered set is the set of natural numbers. An example of set that is not well ordered is the set of integers. To demonstrate the failure of the integers to be well ordered, take the subset of even integers {... -4,-2,0,2,4,...}. This subset has no least element, because subtracting two from an element in the subset gives a smaller element in the set.
Even though the integers under their usual order are not well ordered, the integers can be well ordered if we change the order relation on the set. One such alternative ordering is made by taking the negative integers and collating them with the positive integers, like this {0,1,-1,2,-2,...}.
In mathematics
, the well-ordering principle states that every non-empty set of positive integers contains a smallest element.
Proof: If there exists a non-empty subset A of the set of natural numbers,
for every x in A, , or A is bounded below.
, or A is bounded below.
Therefore, A has an infimum
, say . By the approximation property of the supremum
. By the approximation property of the supremum
of a set of real numbers, for every z > 0, there exists x in A such that . Therefore,
. Therefore, 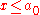 and then
and then  belongs to A for
belongs to A for  .
.
-->
Depending on the framework in which the natural numbers are introduced, this (second order) property of the set of natural numbers is either an axiom
or a provable theorem. For example:
In the second sense, the phrase is used when that proposition is relied on for the purpose of justifying proofs that take the following form: to prove that every natural number belongs to a specified set S, assume the contrary and infer the existence of a (non-zero) smallest counterexample. Then show either that there must be a still smaller counterexample or that the smallest counterexample is not a counter example, producing a contradiction. This mode of argument bears the same relation to proof by mathematical induction
that "If not B then not A" (the style of modus tollens
) bears to "If A then B" (the style of modus ponens
). It is known light-heartedly as the "minimal criminal" method and is similar in its nature to Fermat's method of "infinite descent
".
Garrett Birkhoff
and Saunders Mac Lane
wrote in A Survey of Modern Algebra that this property, like the least upper bound axiom
for real numbers, is non-algebraic; i.e., it cannot be deduced from the algebraic properties of the integers (which form an ordered integral domain).
Even though the integers under their usual order are not well ordered, the integers can be well ordered if we change the order relation on the set. One such alternative ordering is made by taking the negative integers and collating them with the positive integers, like this {0,1,-1,2,-2,...}.
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the well-ordering principle states that every non-empty set of positive integers contains a smallest element.
Proof: If there exists a non-empty subset A of the set of natural numbers,
for every x in A,
 , or A is bounded below.
, or A is bounded below.Therefore, A has an infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
, say
 . By the approximation property of the supremum
. By the approximation property of the supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of a set of real numbers, for every z > 0, there exists x in A such that
 . Therefore,
. Therefore, 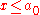 and then
and then  belongs to A for
belongs to A for  .
.-->
Depending on the framework in which the natural numbers are introduced, this (second order) property of the set of natural numbers is either an axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
or a provable theorem. For example:
- In Peano Arithmetic, second-order arithmeticSecond-order arithmeticIn mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
and related systems, and indeed in most (not necessarily formal) mathematical treatments of the well-ordering principle, the principle is derived from the principle of mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, which is itself taken as basic. - Considering the natural numbers as a subset of the real numbers, and assuming that we know already that the real numbers are complete (again, either as an axiom or a theorem about the real number system), i.e., every bounded (from below) set has an infimum, then also every set A of natural numbers has an infimum, say a*. We can now find an integer n* such that a* lies in the half-open interval (n*−1, n*], and can then show that we must have a* = n*, and n* in A.
- In axiomatic set theory, the natural numbers are defined as the smallest inductive setInductive set (axiom of infinity)In the context of the axiom of infinity, an inductive set is a set X with the property that, for every x \in X, the successor x' of x is also an element of X and the set X contains the empty set \varnothing....
(i.e., set containing 0 and closed under the successor operation). One can (even without invoking the regularity axiomAxiom of regularityIn mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
) show that the set of all natural numbers n such that "{0, …, n} is well-ordered" is inductive, and must therefore contain all natural numbers; from this property one can conclude that the set of all natural numbers is also well-ordered.
In the second sense, the phrase is used when that proposition is relied on for the purpose of justifying proofs that take the following form: to prove that every natural number belongs to a specified set S, assume the contrary and infer the existence of a (non-zero) smallest counterexample. Then show either that there must be a still smaller counterexample or that the smallest counterexample is not a counter example, producing a contradiction. This mode of argument bears the same relation to proof by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that "If not B then not A" (the style of modus tollens
Modus tollens
In classical logic, modus tollens has the following argument form:- Formal notation :...
) bears to "If A then B" (the style of modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
). It is known light-heartedly as the "minimal criminal" method and is similar in its nature to Fermat's method of "infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
".
Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
and Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
wrote in A Survey of Modern Algebra that this property, like the least upper bound axiom
Least upper bound axiom
The least upper bound axiom, also abbreviated as the LUB axiom, is an axiom of real analysis stating that the set R of real numbers has the least-upper-bound property. That is, if a nonempty set of real numbers has an upper bound, then it has a least upper bound...
for real numbers, is non-algebraic; i.e., it cannot be deduced from the algebraic properties of the integers (which form an ordered integral domain).

