Von Neumann entropy
Encyclopedia
In quantum statistical mechanics
, von Neumann entropy, named after John von Neumann
, is the extension of classical entropy
concepts to the field of quantum mechanics
.
John von Neumann
rigorously established the correct mathematical framework for quantum mechanics with his work Mathematische Grundlagen der Quantenmechanik. He provided in this work a theory of measurement, where the usual notion of wave collapse is described as an irreversible process (the so called von Neumann or projective measurement).
was introduced, with different motivations, by von Neumann and by Lev Landau
. The motivation that inspired Landau was the impossibility of describing a subsystem of a composite quantum system by a state vector. On the other hand, von Neumann introduced the density matrix in order to develop both quantum statistical mechanics and a theory of quantum measurements.
The density matrix formalism was developed to extend the tools of classical statistical mechanics to the quantum domain. In the classical framework we compute the partition function
of the system in order to evaluate all possible thermodynamic quantities. Von Neumann introduced the density matrix in the context of states and operators in a Hilbert space. The knowledge of the statistical density matrix operator would allow us to compute all average quantities in a conceptually similar, but mathematically different way. Let us suppose we have a set of wave functions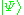
which depend parametrically on a set of quantum numbers 
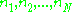. The natural variable which we have is the amplitude with which a
particular wavefunction of the basic set participates in the actual wavefunction of the system. Let us denote the square of this amplitude by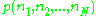
. The goal is to turn this quantity 
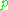into the classical density function in phase space. We have to verify that 
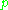goes over into the density function in the classical limit and that it has ergodic properties. After checking that 
is a constant of motion, an ergodic assumption for the probabilities 
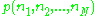makes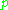 
a function of the energy only .
After this procedure, one finally arrives at the density matrix formalism when seeking a form where
is invariant with respect to the representation used. In the form it is written, it will only yield the correct expectation values for quantities which are diagonal with respect to the quantum numbers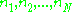 
.
Expectation values of operators which are not diagonal involve the phases of the quantum amplitudes. Suppose we encode the quantum numbers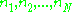
into the single index 
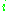or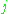 
. Then our wave function has the form
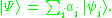
The expectation value of an operator
which is not diagonal in these wave functions, so
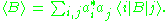
The role which was originally reserved for the quantities
is thus taken over by the density matrix of your system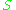 
.
Therefore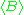
reads as
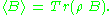
The invariance of the above term is described by matrix theory. We described a mathematical framework where the expectation value of quantum operators, as described by matrices, is obtained by taking the trace of the product of the density operator
and an operator 
(Hilbert scalar product between operators). The matrix formalism here is in the statistical mechanics framework, although it applies as well for finite quantum systems, which is usually the case, where the state of the system cannot be described by a pure state, but as a statistical operator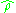 
of the form (\ref{qp1}). Mathematically, 
is a positive, semidefinite hermitian matrix with unit trace.
which is a proper extension of the Gibbs entropy and the Shannon entropy to the quantum case. To compute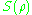
it is convenient to find a basis in which ρ possesses a diagonal representation (see logarithm of a matrix
). If the system is finite (finite dimensional matrix representation) the entropy
describes the departure of our system from a pure state. In other words, it measures the degree of mixture of our state describing a given finite system.
Instead, if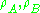
are the reduced density matrices of the general state 
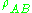, then
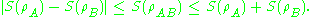
This right hand inequality is known as subadditivity. The two inequalities
together are sometimes known
as the triangle inequality
. They were proved in 1970
by Huzihiro Araki
and Elliott H. Lieb
. While in Shannon's theory the entropy of a composite system can never be lower than the entropy of any of its parts, in quantum theory this is not the case, i.e., it is possible that
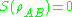while 
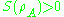and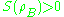 
.
Intuitively, this can be understood as follows: In quantum mechanics, the entropy of the joint system can be less than the sum of the entropy of its components because the components may be entangled
. For instance, the Bell state
of two spin-1/2's,
, is a pure state with zero entropy, but each spin has maximum entropy when considered individually. The entropy in one spin can be "cancelled" by being correlated with the entropy of the other. The left-hand inequality can be roughly interpreted as saying that entropy can only be canceled by an equal amount of entropy. If system 
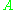and system 
have different amounts of entropy, the lesser can only partially cancel the greater, and some entropy must be left over. Likewise, the right-hand inequality can be interpreted as saying that the entropy of a composite system is maximized when its components are uncorrelated, in which case the total entropy is just a sum of the sub-entropies.
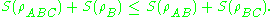
This is a much more difficult theorem and was proved in 1973 by
Elliott H. Lieb
and Mary Beth Ruskai, using a
matrix inequality of Elliott H. Lieb
proved in
1973. By using the proof technique that establishes the left side of the triangle inequality
above, one can show that the strong subadditivity inequality is equivalent to
the following inequality.
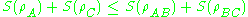
when
, etc. are the reduced density matrices of a density matrix
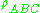. If we apply ordinary subadditivity to the left side of this inequality, and consider all permutations of
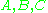, we obtain the triangle inequality
for
: Each of the three numbers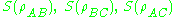 
is less than or equal to the sum of the other two.
, relative entropies, etc.) in the framework of quantum information theory. Entanglement measures are based upon some quantity directly related to the von Neumann entropy. However, there have appeared in the literature several papers dealing with the possible inadequacy of the Shannon information measure, and consequently of the von Neumann entropy as an appropriate quantum generalization of Shannon entropy. The main argument is that in classical measurement the Shannon information measure is a natural measure of our ignorance about the properties of a system, whose existence is independent of measurement
. Conversely, quantum measurement cannot be claimed to reveal the properties of a system that existed before the measurement was made. This controversy has encouraged some authors to introduce the non-additivity
property of Tsallis entropy
(a generalization of the standard Boltzmann–Gibbs entropy) as the main reason for recovering a true quantal information
measure in the quantum context, claiming that non-local correlations ought to be described because of the particularity of Tsallis entropy.
Quantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
, von Neumann entropy, named after John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, is the extension of classical entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
concepts to the field of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
rigorously established the correct mathematical framework for quantum mechanics with his work Mathematische Grundlagen der Quantenmechanik. He provided in this work a theory of measurement, where the usual notion of wave collapse is described as an irreversible process (the so called von Neumann or projective measurement).
Development
The density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
was introduced, with different motivations, by von Neumann and by Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
. The motivation that inspired Landau was the impossibility of describing a subsystem of a composite quantum system by a state vector. On the other hand, von Neumann introduced the density matrix in order to develop both quantum statistical mechanics and a theory of quantum measurements.
The density matrix formalism was developed to extend the tools of classical statistical mechanics to the quantum domain. In the classical framework we compute the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of the system in order to evaluate all possible thermodynamic quantities. Von Neumann introduced the density matrix in the context of states and operators in a Hilbert space. The knowledge of the statistical density matrix operator would allow us to compute all average quantities in a conceptually similar, but mathematically different way. Let us suppose we have a set of wave functions
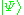which depend parametrically on a set of quantum numbers 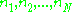. The natural variable which we have is the amplitude with which aparticular wavefunction of the basic set participates in the actual wavefunction of the system. Let us denote the square of this amplitude by
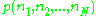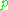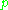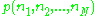. The goal is to turn this quantity into the classical density function in phase space. We have to verify that goes over into the density function in the classical limit and that it has ergodic properties. After checking that is a constant of motion, an ergodic assumption for the probabilities makes 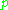a function of the energy only .After this procedure, one finally arrives at the density matrix formalism when seeking a form where
is invariant with respect to the representation used. In the form it is written, it will only yield the correct expectation values for quantities which are diagonal with respect to the quantum numbers 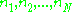.Expectation values of operators which are not diagonal involve the phases of the quantum amplitudes. Suppose we encode the quantum numbers
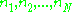into the single index 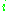or 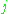. Then our wave function has the form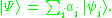The expectation value of an operator
which is not diagonal in these wave functions, so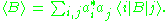The role which was originally reserved for the quantities
is thus taken over by the density matrix of your system 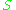.Therefore
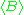reads as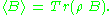The invariance of the above term is described by matrix theory. We described a mathematical framework where the expectation value of quantum operators, as described by matrices, is obtained by taking the trace of the product of the density operator
and an operator (Hilbert scalar product between operators). The matrix formalism here is in the statistical mechanics framework, although it applies as well for finite quantum systems, which is usually the case, where the state of the system cannot be described by a pure state, but as a statistical operator 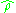of the form (\ref{qp1}). Mathematically, is a positive, semidefinite hermitian matrix with unit trace.Definition
Given the density matrix ρ, von Neumann defined the entropy aswhich is a proper extension of the Gibbs entropy and the Shannon entropy to the quantum case. To compute
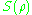it is convenient to find a basis in which ρ possesses a diagonal representation (see logarithm of a matrixLogarithm of a matrix
In mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and...
). If the system is finite (finite dimensional matrix representation) the entropy
describes the departure of our system from a pure state. In other words, it measures the degree of mixture of our state describing a given finite system.Properties
Some properties of the von Neumann entropy:-
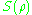is only zero for pure states. -
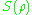is maximal and equal to 
for a maximally mixed state, 
being the dimension of the Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. -
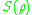is invariant under changes in the basis of 
, that is,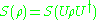 
, with 
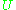a unitary transformation. -
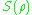is concave, that is, given a collection of positive numbers 
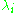which sum to unity (
) and density operators 
, we have
-
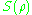is additive. Given two density matrices 
describing independent systems 
and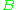 
, then 
.
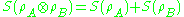Instead, if
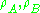are the reduced density matrices of the general state 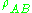, then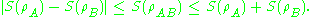This right hand inequality is known as subadditivity. The two inequalities
together are sometimes known
as the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
. They were proved in 1970
by Huzihiro Araki
Huzihiro Araki
is a Japanese mathematical physicist and mathematician.Araki is the son of the University of Kyoto physics professor Gentarō Araki, with whom he studied and with whom in 1954 he published his first physics paper...
and Elliott H. Lieb
Elliott H. Lieb
Elliott H. Lieb is an eminent American mathematical physicist and professor of mathematics and physics at Princeton University who specializes in statistical mechanics, condensed matter theory, and functional analysis....
. While in Shannon's theory the entropy of a composite system can never be lower than the entropy of any of its parts, in quantum theory this is not the case, i.e., it is possible that
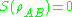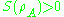while and 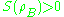.Intuitively, this can be understood as follows: In quantum mechanics, the entropy of the joint system can be less than the sum of the entropy of its components because the components may be entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
. For instance, the Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
of two spin-1/2's,
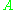, is a pure state with zero entropy, but each spin has maximum entropy when considered individually. The entropy in one spin can be "cancelled" by being correlated with the entropy of the other. The left-hand inequality can be roughly interpreted as saying that entropy can only be canceled by an equal amount of entropy. If system and system have different amounts of entropy, the lesser can only partially cancel the greater, and some entropy must be left over. Likewise, the right-hand inequality can be interpreted as saying that the entropy of a composite system is maximized when its components are uncorrelated, in which case the total entropy is just a sum of the sub-entropies.- The von Neumann entropy is also strongly subadditive. Given three Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s,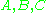
,
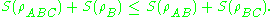
This is a much more difficult theorem and was proved in 1973 by
Elliott H. Lieb
Elliott H. Lieb
Elliott H. Lieb is an eminent American mathematical physicist and professor of mathematics and physics at Princeton University who specializes in statistical mechanics, condensed matter theory, and functional analysis....
and Mary Beth Ruskai, using a
matrix inequality of Elliott H. Lieb
Elliott H. Lieb
Elliott H. Lieb is an eminent American mathematical physicist and professor of mathematics and physics at Princeton University who specializes in statistical mechanics, condensed matter theory, and functional analysis....
proved in
1973. By using the proof technique that establishes the left side of the triangle inequality
above, one can show that the strong subadditivity inequality is equivalent to
the following inequality.
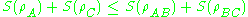
when
, etc. are the reduced density matrices of a density matrix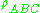. If we apply ordinary subadditivity to the left side of this inequality, and consider all permutations of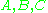, we obtain the triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
for
: Each of the three numbers 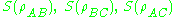is less than or equal to the sum of the other two.Uses
The von Neumann entropy is being extensively used in different forms (conditional entropiesConditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
, relative entropies, etc.) in the framework of quantum information theory. Entanglement measures are based upon some quantity directly related to the von Neumann entropy. However, there have appeared in the literature several papers dealing with the possible inadequacy of the Shannon information measure, and consequently of the von Neumann entropy as an appropriate quantum generalization of Shannon entropy. The main argument is that in classical measurement the Shannon information measure is a natural measure of our ignorance about the properties of a system, whose existence is independent of measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
. Conversely, quantum measurement cannot be claimed to reveal the properties of a system that existed before the measurement was made. This controversy has encouraged some authors to introduce the non-additivity
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
property of Tsallis entropy
Tsallis entropy
In physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
(a generalization of the standard Boltzmann–Gibbs entropy) as the main reason for recovering a true quantal information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
measure in the quantum context, claiming that non-local correlations ought to be described because of the particularity of Tsallis entropy.