
Volterra operator
Encyclopedia
In mathematics
, in the area of functional analysis
and operator theory
, the Volterra operator, named after Vito Volterra
, represents the operation of indefinite integration, viewed as a bounded linear operator on the space L2(0,1) of complex-valued square integrable functions on the interval (0,1). It is the operator corresponding to the Volterra integral equation
s.

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, the Volterra operator, named after Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
, represents the operation of indefinite integration, viewed as a bounded linear operator on the space L2(0,1) of complex-valued square integrable functions on the interval (0,1). It is the operator corresponding to the Volterra integral equation
Volterra integral equation
In mathematics, the Volterra integral equations are a special type of integral equations. They are divided into two groups referred to as the first and the second kind.A linear Volterra equation of the first kind is f = \int_a^t K\,x\,ds...
s.
Definition
The Volterra operator, V, may be defined for a function f(s) ∈ L2(0,1) and a value t ∈ (0,1), as
Properties
- V is a bounded linear operator between Hilbert spaces, with Hermitian adjointHermitian adjointIn mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
-
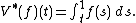
- V is a Hilbert-Schmidt operator, hence in particular is compactCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
. - V has no eigenvalues and therefore, by the spectral theory of compact operatorsSpectral theory of compact operatorsIn functional analysis, compact operators are linear operators that map bounded sets to precompact sets. The set of compact operators acting on a Hilbert space H is the closure of the set of finite rank operators in the uniform operator topology. In general, operators on infinite dimensional spaces...
, its spectrumSpectrum (functional analysis)In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
σ(V) = {0}. - V is a quasinilpotent operator (that is, the spectral radiusSpectral radiusIn mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
, ρ(V), is zero), but it is not nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
. - The operator normOperator normIn mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
of V is exactly ||V|| = 2⁄π.
- V is a Hilbert-Schmidt operator, hence in particular is compact

