
Volterra Series
Encyclopedia
The Volterra series is a model for non-linear behavior similar to the Taylor series
. It differs from the Taylor series in its ability to capture 'memory' effects. The Taylor series can be used to approximate the response of a nonlinear system to a given input if the output of this system depends strictly on the input at that particular time. In the Volterra series the output of the nonlinear system depends on the input to the system at all other times. This provides the ability to capture the 'memory' effect of devices such as capacitors and inductors.
It has been applied in the fields of medicine (biomedical engineering) and biology, especially neuroscience. It is also used in electrical engineering to model intermodulation
distortion in many devices including power amplifiers and frequency mixer
s. Its main advantage lies in its generality: it can represent a wide range of systems. It is therefore sometimes referred to as a non-parametric model.
In mathematics
, a Volterra series denotes a functional expansion of a dynamic, nonlinear, time-invariant functional
. Volterra series are frequently used in system identification
. The Volterra series, which is used to prove the Volterra theorem, is a series of infinite sum of multidimensional convolutional integrals.
in work dating from 1887. Norbert Wiener
became interested in this theory in the 1920's from contact with Volterra's student Paul Lévy
. He applied his theory of the Brownian motion to the integration of Volterra analytic functionals.
The use of Volterra series for system analysis originated from a restricted 1942 wartime report of Wiener, then professor of mathematics at MIT
. It used the series to make an approximate analysis of the effect of radar noise in a nonlinear receiver circuit. The report became public after the war. As a general method of analysis of nonlinear systems, Volterra series came into use after about 1957 as the result of a series of reports, at first privately circulated, from MIT and elsewhere. The name Volterra series came into use a few years later.
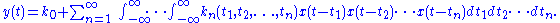
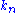 is called the n-th order Volterra kernel
is called the n-th order Volterra kernel
which can be regarded as a higher-order impulse response of the system. Sometimes the nth order term is divided by n!, a convention which is convenient when considering the combination of Volterra systems by placing one after the other ('cascading').
The causality condition: Since in any physically realizable system the output can only depend on previous values of the input, the kernels will be zero if any of the variables
will be zero if any of the variables 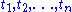 are negative. The integrals may then be written over the half range from zero to infinity.
are negative. The integrals may then be written over the half range from zero to infinity.
's theorem states, that this system can be approximated uniformly and to an arbitrary degree of precision by a sufficiently high, but finite order Volterra series. The input set over which this approximation holds encompasses all equicontinuous, uniformly bounded functions. In physically realizable setting this constraint on the input set should always hold.
, and then recomputing the coefficients of the original Volterra series. The Volterra series main appeal over the orthogonalized series lies in its intuitive, canonical structure, i.e. all interactions of the input have one fixed degree. The orthogonalized basis functionals will generally be quite complicated.
An important aspect, with respect to which the following methods differ is whether the orthogonalization of the basis functionals is to be performed over the idealized specification of the input signal (e.g. gaussian, white noise) or over the actual realization of the input (i.e. the pseudo-random, bounded, almost-white version of gaussian white noise, or any other stimulus). The latter methods, despite their lack of mathematical elegance, have been shown to be more flexible (as arbitrary inputs can be easily accommodated) and precise (due to the effect that the idealized version of the input signal is not always realizable).
. Consequently, this approach is also based on minimizing the empirical error (often called empirical risk minimization). Franz and Schölkopf proposed that the kernel method could essentially replace the Volterra series representation, although noting that the latter is more intuitive.
s to sample the Volterra coefficients.
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. It differs from the Taylor series in its ability to capture 'memory' effects. The Taylor series can be used to approximate the response of a nonlinear system to a given input if the output of this system depends strictly on the input at that particular time. In the Volterra series the output of the nonlinear system depends on the input to the system at all other times. This provides the ability to capture the 'memory' effect of devices such as capacitors and inductors.
It has been applied in the fields of medicine (biomedical engineering) and biology, especially neuroscience. It is also used in electrical engineering to model intermodulation
Intermodulation
Intermodulation or intermodulation distortion is the amplitude modulation of signals containing two or more different frequencies in a system with nonlinearities...
distortion in many devices including power amplifiers and frequency mixer
Frequency mixer
In electronics a mixer or frequency mixer is a nonlinear electrical circuit that creates new frequencies from two signals applied to it. In its most common application, two signals at frequencies f1 and f2 are applied to a mixer, and it produces new signals at the sum f1 + f2 and difference f1 -...
s. Its main advantage lies in its generality: it can represent a wide range of systems. It is therefore sometimes referred to as a non-parametric model.
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Volterra series denotes a functional expansion of a dynamic, nonlinear, time-invariant functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
. Volterra series are frequently used in system identification
System identification
In control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...
. The Volterra series, which is used to prove the Volterra theorem, is a series of infinite sum of multidimensional convolutional integrals.
History
Volterra series is a modernized version of the theory of analytic functionals due to the Italian mathematician Vito VolterraVito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
in work dating from 1887. Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
became interested in this theory in the 1920's from contact with Volterra's student Paul Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
. He applied his theory of the Brownian motion to the integration of Volterra analytic functionals.
The use of Volterra series for system analysis originated from a restricted 1942 wartime report of Wiener, then professor of mathematics at MIT
Massachusetts Institute of Technology
The Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
. It used the series to make an approximate analysis of the effect of radar noise in a nonlinear receiver circuit. The report became public after the war. As a general method of analysis of nonlinear systems, Volterra series came into use after about 1957 as the result of a series of reports, at first privately circulated, from MIT and elsewhere. The name Volterra series came into use a few years later.
Mathematical theory
The theory of Volterra series can be viewed from two different perspectives: either one considers an operator mapping between two real (or complex) function spaces or a functional mapping from a real (or complex) function space into the real (or complex) numbers. The latter, functional perspective is in more frequent use, due to the assumed time-invariance of the system.Continuous time
A continuous time-invariant system with x(t) as input and y(t) as output can be expanded in Volterra series as: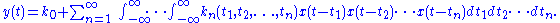
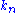 is called the n-th order Volterra kernel
is called the n-th order Volterra kernelKernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
which can be regarded as a higher-order impulse response of the system. Sometimes the nth order term is divided by n!, a convention which is convenient when considering the combination of Volterra systems by placing one after the other ('cascading').
The causality condition: Since in any physically realizable system the output can only depend on previous values of the input, the kernels
 will be zero if any of the variables
will be zero if any of the variables 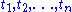 are negative. The integrals may then be written over the half range from zero to infinity.
are negative. The integrals may then be written over the half range from zero to infinity.Discrete time
Let F be a continuous functional system, which is time-invariant and has finite memory. Then FréchetMaurice René Fréchet
Maurice Fréchet was a French mathematician. He made major contributions to the topology of point sets and introduced the entire concept of metric spaces. He also made several important contributions to the field of statistics and probability, as well as calculus...
's theorem states, that this system can be approximated uniformly and to an arbitrary degree of precision by a sufficiently high, but finite order Volterra series. The input set over which this approximation holds encompasses all equicontinuous, uniformly bounded functions. In physically realizable setting this constraint on the input set should always hold.
Methods to estimate the Kernel coefficients
Estimating the Volterra coefficients individually is complicated since the basis functionals of the Volterra series are correlated. This leads to the problem of simultaneously solving a set of integral-equations for the coefficients. Hence, estimation of Volterra coefficients is generally performed by estimating the coefficients of an orthogonalized series, e.g. the Wiener seriesWiener series
In mathematics, the Wiener series originates from the 1958 book of Norbert Wiener. It is an orthogonal expansion for nonlinear functionals closely related to the Volterra series and having the same relation to it as an orthogonal polynomial expansion has to a power series. The analogue of the...
, and then recomputing the coefficients of the original Volterra series. The Volterra series main appeal over the orthogonalized series lies in its intuitive, canonical structure, i.e. all interactions of the input have one fixed degree. The orthogonalized basis functionals will generally be quite complicated.
An important aspect, with respect to which the following methods differ is whether the orthogonalization of the basis functionals is to be performed over the idealized specification of the input signal (e.g. gaussian, white noise) or over the actual realization of the input (i.e. the pseudo-random, bounded, almost-white version of gaussian white noise, or any other stimulus). The latter methods, despite their lack of mathematical elegance, have been shown to be more flexible (as arbitrary inputs can be easily accommodated) and precise (due to the effect that the idealized version of the input signal is not always realizable).
Crosscorrelation method
This method, developed by Lee & Schetzen, orthogonalizes with respect to the actual mathematical description of the signal, i.e. the projection onto the new basis functionals is based on the knowledge of the moments of the random signal.Exact orthogonal algorithm
This method and its more efficient version (Fast Orthogonal Algorithm) were invented by Korenberg. In this method the orthogonalization is performed empirically over the actual input. It has been shown to perform more precisely than the Crosscorrelation method. Another advantage is that arbitrary inputs can be used for the orthogonalization and that fewer data-points suffice to reach a desired level of accuracy. Also, estimation can be performed incrementally until some criterion is fulfilled.Linear regression
Linear regression is a standard tool from linear analysis. Hence, one of its main advantages is the widespread existence of standard tools for solving linear regressions efficiently. It has some educational value, since it highlights the basic property of Volterra series: linear combination of non-linear basis-functionals. For estimation the order of the original should be known, since the volterra basis-functionals are not orthogonal and estimation can thus not be performed incrementally.Kernel method
This method was invented by Franz & Schölkopf and is based on statistical learning theoryStatistical learning theory
Statistical learning theory is an ambiguous term.#It may refer to computational learning theory, which is a sub-field of theoretical computer science that studies how algorithms can learn from data....
. Consequently, this approach is also based on minimizing the empirical error (often called empirical risk minimization). Franz and Schölkopf proposed that the kernel method could essentially replace the Volterra series representation, although noting that the latter is more intuitive.
Differential sampling
This method was developed by van Hemmen and coworkers and utilizes Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
s to sample the Volterra coefficients.

