
Visual angle illusion
Encyclopedia
In human visual perception
, the visual angle
, denoted θ, subtended by a viewed object sometimes looks larger or smaller than its actual value. One approach to this phenomenon posits a subjective correlate to the visual angle: the perceived visual angle or perceived angular size. An optical illusion
where the physical and subjective angles differ is then called a visual angle illusion or angular size illusion.
Angular size illusions are most obvious as relative angular size illusions, in which two objects that subtend the same visual angle appear to have different angular sizes; it is as if their equal-sized images on the retina
were of different sizes. Angular size illusions are contrasted with linear size illusions, in which two objects that are the same physical size do not appear so. An angular size illusion may be accompanied by (or cause) a linear size illusion at the same time.
The perceived visual angle paradigm
begins with a rejection of the classical size-distance invariance hypothesis (SDIH), which states that the ratio of perceived linear size to perceived distance is a simple function of the visual angle. The SDIH does not explain some illusions, such as the Moon illusion
, in which the Moon appears larger when it is near the horizon. It is replaced by a perceptual SDIH, in which the visual angle is replaced by the perceived visual angle. This new formulation avoids some of the paradoxes of the SDIH, but it remains difficult to explain why a given illusion occurs.
This paradigm is not universally accepted; many textbook explanations of size and distance perception do not refer to the perceived visual angle, and some researchers deny that it exists. Some recent evidence supporting the idea, reported by Murray, Boyaci and Kersten (2006), suggests a direct relationship between the perceived angular size of an object and the size of the neural activity pattern it excites in the primary visual cortex.
Indeed, various experiments have revealed most of the factors responsible for these visual angle illusions, and a few different explanations for them have been published (Baird, Wagner, & Fuld, 1990, Enright, 1987, 1989, Hershenson, 1982, 1989, Komoda & Ono, 1974, McCready, 1965, 1985, 1986, 1994, Ono, 1970, Oyama, 1977, Reed, 1984, 1989, Restle, 1970, Roscoe, 1985, 1989).
On the other hand, nearly all discussions (and explanations) of those classic size illusions found in textbooks, the popular media, and on the internet use, instead, an older hypothesis that the visual angle is not perceivable (Gregory, 2008, Kaufman & Kaufman, 2002). They can describe and explain only a linear size illusion, which is why they do not properly describe or explain the illusions that most people experience.
In order to clarify the new paradigm which replaces the old one, it helps to keep in mind that an angle
is the difference between two directions from a common point (the vertex). Accordingly, as described below, the visual angle θ is the difference between two real (optical) directions in the field of view
, while the perceived visual angle θ′, is the difference by which the directions of two viewed points from oneself appear to differ in the visual field
.
.
The line from B through O indicates the chief ray of the bundle of light rays that form the optical image of B on the retina
at point b, let's say, on the fovea
. Likewise, endpoint A is imaged at point a.
The optical (physical) angle between those chief rays is the visual angle θ which can be calculated:
The retinal images at b and a are separated by the distance R, given by the equation
in which n is the eye's nodal distance that averages about . That is, a viewed object's retinal image size is approximately given by .
The line from point O outward through object point B specifies the optical direction, dB, of the object's base from the eye, let's say toward the horizon
. The line from point O through point A specifies that endpoint's optical direction, dA, toward some specific elevation value (say, 18 degrees). The difference between those real directions (dA - dB) is, again, the visual angle θ.
Point O′ represents the place from which the observer feels that he or she is viewing the world. For present purposes, O′ can represent the cyclopean eye (Ono, 1970, Ono, Mapp & Howard, 2002).
Similarly, S′ is the perceived linear extent by which the subjective point A′ appears directly above point B′. The observer could simply say how many inches or meters that vertical distance looks. For a viewed object, S′ thus is its perceived linear size in meters, (or apparent linear size).
This concept of the (subjective) visual direction is very old. However, as Wade, Ono & Mapp (2006) noted, it unfortunately has been ignored in many current theories of size perception, and size illusions.
The object's other perceived endpoint, A′, has a perceived direction d′A;, about which the observer might say "it appears toward a higher elevation than point B′." The difference between the two perceived directions (d′A - d′B) is the perceived visual angle θ′, also called the perceived angular size or apparent angular size.
It is not easy to quantify θ′. For instance, a well-trained observer might say that point A′ "looks about 25 degrees higher" than B′, but most cannot reliably say how large a direction difference looks. That skill is not practiced because it is easier to use pointing gestures (Ono, 1970): For example, one often tells another person about the change in the directions seen for two viewed points by pointing something, say a finger or the eyes from one point to the other.
Therefore, in some experiments the observers aimed a pointer from one viewed point to the other, so the angle through which the pointer rotated was the measure of θ′, (Komodo, 1970, Komodo & Ono, 1974, Ono, Muter, & Mitson, 1974, Gogel & Eby, 1997).
Also, because θ′, specifies the amount by which one should rotate one's eye to quickly look from one seen point to another eye tracking
, saccade
, observers in other experiments shifted their gaze from one object endpoint to the other, and the angle the eye rotated through was measured as θ′ for that object (Yarbus (1967).
Suppose one is looking through a window at a 30 feet (9.1 m) house 240 feet away, so it subtends a visual angle of about 7 degrees. The 30 inches (762 mm) window opening is 10 feet away, so it subtends a visual angle of 14 degrees.
It can be said that the house "looks larger and farther away" than the window, meaning that the perceived linear size S′ for the house's width is much larger than S′ for the window; for instance a person might say the house "looks about 40 feet wide" and the window "looks about 3 feet wide."
One can also say that the house "looks smaller and farther away" than the window, and that does not contradict the other statement because now we mean that the amount (θ′) by which directions of the house's edges appear to differ is, say, about half the apparent direction difference for the window edges.
Notice that humans experience both the linear size and the angular size comparisons at the same time, along with the distance comparison (Joynson, 1949). Thus any report merely that one object "looks larger" than another object is ambiguous. It needs to specify whether "looks larger" refers to the perceived angular size (θ′) or to the perceived linear size (S′) or to both of those qualitatively different "size" experiences (Joynson, 1949, McCready, 1965, 1985, Ono, 1970). Notice that in everyday conversations "looks larger" often refers to an angular size comparison rather than a linear size comparison.
Additional confusion has resulted from widespread use of the ambiguous terms "apparent size" and "perceived size", because they sometimes have referred to θ′ and sometimes to S′ without clarification, so the reader must try to ascertain what they mean. Also, in astronomy, "apparent size" refers to the physical angle θ rather than to the subjective apparent visual angle θ′.

Ross & Plug (2002, Page 31) dubbed this new rule the "perceptual size-distance invariance hypothesis".
l image normally determines the extent of the neural activity pattern the retina's neural activity eventually generates in the primary visual cortex, area V1 or Brodmann area 17. This cortical area harbors a distorted but spatially isomorphic "map" of the retina (see Retinotopy
). This neurological relationship recently was confirmed by Murray, Boyaci, & Kersten (2006) using functional magnetic resonance imaging
.
The retinal image is not perceived or sensed. That is, experimental psychologists long ago rejected any idea that people "sense" a proximal stimulus such as the retinal image. As Gogel (1969, 1997) has repeatedly emphasized, there is no "sensation" which could be called the "perceived retinal image size," R′.
Also rejected is a popular idea that an object's "perceived size" results from a "scaling of retinal size;" an illogical process that somehow "magnifies" the very small "retinal size" to yield the viewed object's much larger perceived linear size S′.
Instead, the physical retinal extent R normally determines the magnitude of the perceived visual angle θ′. But, as already noted, "other factors" can intervene to slightly change θ′ for a target forming a constant sized retinal image (and thereby create a visual angle illusion). Indeed, the major discovery by Murray et al. (2006) concerns this flexible relationship between R and θ′, as described below.
The researchers pointed out that their findings dramatically disagree with the hypothetical models of neural events being proposed in nearly all current theories of visual spatial perception.
Murray, et al. (2006) also noted that the flat illusion pattern they used can represent other classic "size" illusions, such as the Ponzo illusion
and, as well, the moon illusion
which is a visual angle illusion for most observers, (McCready, 1965, 1986, Restle 1970, Plug & Ross, 1989, p. 21, Ross & Plug, 2002).
A detailed meta-analysis of the Murray et al. (2006) results is available in McCready (2007, Appendix B).
That old SDIH logic (geometry) is typically illustrated using a diagram that resembles Figure 2, but has the physical visual angle θ substituted for the perceived visual angle θ′. The equation for the SDIH thus is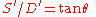
Here, S′ is typically called the "perceived size" or "apparent size"; more precisely it is the perceived linear size, measured in meters.
When rearranged as S′ = D′ tan θ, the equation expresses Emmert's law
.
However, at least since 1962, researchers have pointed out that many classic "size" and distance illusions 3 can be neither described nor explained using the SDIH, so a new hypothesis is needed (Boring 1962, Gruber, 1956, McCready, 1965, Baird, 1970, Ono 1970). For instance, consider the simple Ebbinghaus illusion.
According to the SDIH, "looks larger" can mean only that S′ is greater, and with the physical angle θ the same for both, the SDIH requires that D′ be greater for the lower one than for the upper one. However, for most observers, both circles appear unequal while also appearing at the same distance (on the same page).
This commonly found disagreement between published data and the SDIH is known as the "size-distance paradox" (Gruber, 1956, Ono, et al. 1974).
The "paradox" completely vanishes, however, when the illusion is described, instead, as basically a visual angle illusion: That is, the perceived visual angle θ′ is larger for the lower circle than for the upper circle: It is as if its retinal image were larger.
So. according to the "new" perceptual invariance hypothesis, (S′/D′ = tan θ′), with θ′ larger for the lower circle, and with D′ correctly the same for both circles, then S′ becomes larger for the lower one by the same ratio that θ′ is larger. That is, the reason the lower one looks a larger linear size on the page is because it looks a larger angular size than the upper one.
Describing the few existing explanations for visual angle illusions is beyond the scope of this present entry. The most recent theories have been presented mostly in articles concerning the moon illusion (Baird et al., 1990, Enright, 1989a, 1989b, Hershenson, 1982, 1989b, Higashiyama, 1992, McCready 1986, 1999-2007, Plug & Ross, 1989, Reed, 1989, Roscoe, 1989, and especially in two "moon illusion" books (Hershenson, 1989; Ross & Plug, 2002) which make it quite clear that vision scientists have not yet agreed upon any particular theory of visual angle illusions.
There also is the lesser-known, but evidently the largest visual angle illusion of oculomotor micropsia (convergence micropsia
) for which a few different explanations are being considered (McCready, 1965, 2007, Ono, 1970, Komoda & Ono, 1974, Ono, et al. 1974, Enright, 1987b, 1989a, 1989b).
This is a partial list of "size and distance" illusions that begin as visual angle illusions (angular size illusions) for most observers.
Visual perception
Visual perception is the ability to interpret information and surroundings from the effects of visible light reaching the eye. The resulting perception is also known as eyesight, sight, or vision...
, the visual angle
Visual angle
The visual angle is the angle a viewed object subtends at the eye, usually stated in degrees of arc.It also is called the object's angular size....
, denoted θ, subtended by a viewed object sometimes looks larger or smaller than its actual value. One approach to this phenomenon posits a subjective correlate to the visual angle: the perceived visual angle or perceived angular size. An optical illusion
Optical illusion
An optical illusion is characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a perception that does not tally with a physical measurement of the stimulus source...
where the physical and subjective angles differ is then called a visual angle illusion or angular size illusion.
Angular size illusions are most obvious as relative angular size illusions, in which two objects that subtend the same visual angle appear to have different angular sizes; it is as if their equal-sized images on the retina
Retina
The vertebrate retina is a light-sensitive tissue lining the inner surface of the eye. The optics of the eye create an image of the visual world on the retina, which serves much the same function as the film in a camera. Light striking the retina initiates a cascade of chemical and electrical...
were of different sizes. Angular size illusions are contrasted with linear size illusions, in which two objects that are the same physical size do not appear so. An angular size illusion may be accompanied by (or cause) a linear size illusion at the same time.
The perceived visual angle paradigm
Paradigm
The word paradigm has been used in science to describe distinct concepts. It comes from Greek "παράδειγμα" , "pattern, example, sample" from the verb "παραδείκνυμι" , "exhibit, represent, expose" and that from "παρά" , "beside, beyond" + "δείκνυμι" , "to show, to point out".The original Greek...
begins with a rejection of the classical size-distance invariance hypothesis (SDIH), which states that the ratio of perceived linear size to perceived distance is a simple function of the visual angle. The SDIH does not explain some illusions, such as the Moon illusion
Moon illusion
The Moon illusion is an optical illusion in which the Moon appears larger near the horizon than it does while higher up in the sky. This optical illusion also occurs with the sun and star constellations. It has been known since ancient times, and recorded by numerous different cultures...
, in which the Moon appears larger when it is near the horizon. It is replaced by a perceptual SDIH, in which the visual angle is replaced by the perceived visual angle. This new formulation avoids some of the paradoxes of the SDIH, but it remains difficult to explain why a given illusion occurs.
This paradigm is not universally accepted; many textbook explanations of size and distance perception do not refer to the perceived visual angle, and some researchers deny that it exists. Some recent evidence supporting the idea, reported by Murray, Boyaci and Kersten (2006), suggests a direct relationship between the perceived angular size of an object and the size of the neural activity pattern it excites in the primary visual cortex.
A relatively new idea
Visual angle illusions have been explicitly described by many vision researchers, including , , , Baird (1970), Ono (1970), Roscoe (1985, 1989), Hershenson (1982, 1989), Reed (1984, 1989), Enright (1989), Plug & Ross (1989, 1994), Higashiyama & Shimono (1994), Gogel, & Eby (1997), Ross & Plug (2002), and Murray, Boyaci & Kersten (2006). Specifically, these researchers cited have advocated a relatively new idea: that many of the best-known size illusions (see Note 3) demonstrate that for most observers the (subjective) perceived visual angle, θ′, can change for a viewed target that subtends a constant (physical) visual angle θ.Indeed, various experiments have revealed most of the factors responsible for these visual angle illusions, and a few different explanations for them have been published (Baird, Wagner, & Fuld, 1990, Enright, 1987, 1989, Hershenson, 1982, 1989, Komoda & Ono, 1974, McCready, 1965, 1985, 1986, 1994, Ono, 1970, Oyama, 1977, Reed, 1984, 1989, Restle, 1970, Roscoe, 1985, 1989).
On the other hand, nearly all discussions (and explanations) of those classic size illusions found in textbooks, the popular media, and on the internet use, instead, an older hypothesis that the visual angle is not perceivable (Gregory, 2008, Kaufman & Kaufman, 2002). They can describe and explain only a linear size illusion, which is why they do not properly describe or explain the illusions that most people experience.
In order to clarify the new paradigm which replaces the old one, it helps to keep in mind that an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
is the difference between two directions from a common point (the vertex). Accordingly, as described below, the visual angle θ is the difference between two real (optical) directions in the field of view
Field of view
The field of view is the extent of the observable world that is seen at any given moment....
, while the perceived visual angle θ′, is the difference by which the directions of two viewed points from oneself appear to differ in the visual field
Visual field
The term visual field is sometimes used as a synonym to field of view, though they do not designate the same thing. The visual field is the "spatial array of visual sensations available to observation in introspectionist psychological experiments", while 'field of view' "refers to the physical...
.
Physical measures S, D, R, and θ
Figure 1 illustrates an observer's eye looking at a frontal extent AB that has a linear size S (also called its "metric size" or "tape-measure size"). The extent's lower endpoint at B lies at a distance D from point O, which for present purposes can represent the center of the eye's entrance pupilEntrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
.
The line from B through O indicates the chief ray of the bundle of light rays that form the optical image of B on the retina
Retina
The vertebrate retina is a light-sensitive tissue lining the inner surface of the eye. The optics of the eye create an image of the visual world on the retina, which serves much the same function as the film in a camera. Light striking the retina initiates a cascade of chemical and electrical...
at point b, let's say, on the fovea
Fovea
The fovea centralis, also generally known as the fovea , is a part of the eye, located in the center of the macula region of the retina....
. Likewise, endpoint A is imaged at point a.
The optical (physical) angle between those chief rays is the visual angle θ which can be calculated:

The retinal images at b and a are separated by the distance R, given by the equation

in which n is the eye's nodal distance that averages about . That is, a viewed object's retinal image size is approximately given by .
The line from point O outward through object point B specifies the optical direction, dB, of the object's base from the eye, let's say toward the horizon
Horizon
The horizon is the apparent line that separates earth from sky, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting...
. The line from point O through point A specifies that endpoint's optical direction, dA, toward some specific elevation value (say, 18 degrees). The difference between those real directions (dA - dB) is, again, the visual angle θ.
Perceived measures
Figure 2 diagrams the perceived (subjective) values for a viewed object.Point O′ represents the place from which the observer feels that he or she is viewing the world. For present purposes, O′ can represent the cyclopean eye (Ono, 1970, Ono, Mapp & Howard, 2002).
Perceived linear values D′ and S′
In Figure 2, D′ is the perceived distance of the subjective point B′ from O′. The observer might simply say how far away point B′ looks, in inches or meters or miles.Similarly, S′ is the perceived linear extent by which the subjective point A′ appears directly above point B′. The observer could simply say how many inches or meters that vertical distance looks. For a viewed object, S′ thus is its perceived linear size in meters, (or apparent linear size).
Perceived visual angle θ′
The perceived endpoint at B′ has the perceived direction, d′B, and the observer might simply say "it looks straight ahead and toward the horizon."This concept of the (subjective) visual direction is very old. However, as Wade, Ono & Mapp (2006) noted, it unfortunately has been ignored in many current theories of size perception, and size illusions.
The object's other perceived endpoint, A′, has a perceived direction d′A;, about which the observer might say "it appears toward a higher elevation than point B′." The difference between the two perceived directions (d′A - d′B) is the perceived visual angle θ′, also called the perceived angular size or apparent angular size.
It is not easy to quantify θ′. For instance, a well-trained observer might say that point A′ "looks about 25 degrees higher" than B′, but most cannot reliably say how large a direction difference looks. That skill is not practiced because it is easier to use pointing gestures (Ono, 1970): For example, one often tells another person about the change in the directions seen for two viewed points by pointing something, say a finger or the eyes from one point to the other.
Therefore, in some experiments the observers aimed a pointer from one viewed point to the other, so the angle through which the pointer rotated was the measure of θ′, (Komodo, 1970, Komodo & Ono, 1974, Ono, Muter, & Mitson, 1974, Gogel & Eby, 1997).
Also, because θ′, specifies the amount by which one should rotate one's eye to quickly look from one seen point to another eye tracking
Eye tracking
Eye tracking is the process of measuring either the point of gaze or the motion of an eye relative to the head. An eye tracker is a device for measuring eye positions and eye movement. Eye trackers are used in research on the visual system, in psychology, in cognitive linguistics and in product...
, saccade
Saccade
A saccade is a fast movement of an eye, head or other part of an animal's body or device. It can also be a fast shift in frequency of an emitted signal or other quick change. Saccades are quick, simultaneous movements of both eyes in the same direction...
, observers in other experiments shifted their gaze from one object endpoint to the other, and the angle the eye rotated through was measured as θ′ for that object (Yarbus (1967).
Difference between θ′ and S′
It is important to understand how θ′ differs from S′. Consider an example illustrated by the sketch at the right.Suppose one is looking through a window at a 30 feet (9.1 m) house 240 feet away, so it subtends a visual angle of about 7 degrees. The 30 inches (762 mm) window opening is 10 feet away, so it subtends a visual angle of 14 degrees.
It can be said that the house "looks larger and farther away" than the window, meaning that the perceived linear size S′ for the house's width is much larger than S′ for the window; for instance a person might say the house "looks about 40 feet wide" and the window "looks about 3 feet wide."
One can also say that the house "looks smaller and farther away" than the window, and that does not contradict the other statement because now we mean that the amount (θ′) by which directions of the house's edges appear to differ is, say, about half the apparent direction difference for the window edges.
Notice that humans experience both the linear size and the angular size comparisons at the same time, along with the distance comparison (Joynson, 1949). Thus any report merely that one object "looks larger" than another object is ambiguous. It needs to specify whether "looks larger" refers to the perceived angular size (θ′) or to the perceived linear size (S′) or to both of those qualitatively different "size" experiences (Joynson, 1949, McCready, 1965, 1985, Ono, 1970). Notice that in everyday conversations "looks larger" often refers to an angular size comparison rather than a linear size comparison.
Additional confusion has resulted from widespread use of the ambiguous terms "apparent size" and "perceived size", because they sometimes have referred to θ′ and sometimes to S′ without clarification, so the reader must try to ascertain what they mean. Also, in astronomy, "apparent size" refers to the physical angle θ rather than to the subjective apparent visual angle θ′.
The perceptual size-distance invariance hypothesis
How the three perceived values θ′, S′, and D′ would be expected to relate to each other for a given object is illustrated by Figure 2 and stated by the following equation (McCready, 1965, 1985, Ono, 1970, Komoda and Ono, 1974, Reed, 1989, Kaneko & Uchikawa, 1997).
Ross & Plug (2002, Page 31) dubbed this new rule the "perceptual size-distance invariance hypothesis".
Retinal size, "cortical size" and θ′
As already noted, the magnitude of an object's visual angle θ determines the size R of its retinal image. And, the size of the retinaRetina
The vertebrate retina is a light-sensitive tissue lining the inner surface of the eye. The optics of the eye create an image of the visual world on the retina, which serves much the same function as the film in a camera. Light striking the retina initiates a cascade of chemical and electrical...
l image normally determines the extent of the neural activity pattern the retina's neural activity eventually generates in the primary visual cortex, area V1 or Brodmann area 17. This cortical area harbors a distorted but spatially isomorphic "map" of the retina (see Retinotopy
Retinotopy
Retinotopy describes the spatial organization of the neuronal responses to visual stimuli. In many locations within the brain, adjacent neurons have receptive fields that include slightly different, but overlapping portions of the visual field. The position of the center of these receptive fields...
). This neurological relationship recently was confirmed by Murray, Boyaci, & Kersten (2006) using functional magnetic resonance imaging
Functional magnetic resonance imaging
Functional magnetic resonance imaging or functional MRI is a type of specialized MRI scan used to measure the hemodynamic response related to neural activity in the brain or spinal cord of humans or other animals. It is one of the most recently developed forms of neuroimaging...
.
The retinal image is not perceived or sensed. That is, experimental psychologists long ago rejected any idea that people "sense" a proximal stimulus such as the retinal image. As Gogel (1969, 1997) has repeatedly emphasized, there is no "sensation" which could be called the "perceived retinal image size," R′.
Also rejected is a popular idea that an object's "perceived size" results from a "scaling of retinal size;" an illogical process that somehow "magnifies" the very small "retinal size" to yield the viewed object's much larger perceived linear size S′.
Instead, the physical retinal extent R normally determines the magnitude of the perceived visual angle θ′. But, as already noted, "other factors" can intervene to slightly change θ′ for a target forming a constant sized retinal image (and thereby create a visual angle illusion). Indeed, the major discovery by Murray et al. (2006) concerns this flexible relationship between R and θ′, as described below.
Visual angle illusions and area V1
The Murray, et al. (2006) observers viewed a flat picture with two disks that subtended the same visual angle θ and formed retinal images of the same size (R), but the perceived angular size, θ′, for one disk was larger than θ′ for the other (say, 17% larger) due to differences in their background patterns. And, in cortical Area V1, the sizes of the activity patterns related to the disks were unequal, despite the fact that the retinal images were the same size. The difference between these "cortical sizes" in Area V1 for the illusion disks was essentially the same as the difference produced by two non-illusory disks whose retinal image sizes differed by, say, 17%.The researchers pointed out that their findings dramatically disagree with the hypothetical models of neural events being proposed in nearly all current theories of visual spatial perception.
Murray, et al. (2006) also noted that the flat illusion pattern they used can represent other classic "size" illusions, such as the Ponzo illusion
Ponzo illusion
The Ponzo illusion is a geometrical-optical illusion that was first demonstrated by the Italian psychologist Mario Ponzo in 1913. He suggested that the human mind judges an object's size based on its background. He showed this by drawing two identical lines across a pair of converging lines,...
and, as well, the moon illusion
Moon illusion
The Moon illusion is an optical illusion in which the Moon appears larger near the horizon than it does while higher up in the sky. This optical illusion also occurs with the sun and star constellations. It has been known since ancient times, and recorded by numerous different cultures...
which is a visual angle illusion for most observers, (McCready, 1965, 1986, Restle 1970, Plug & Ross, 1989, p. 21, Ross & Plug, 2002).
A detailed meta-analysis of the Murray et al. (2006) results is available in McCready (2007, Appendix B).
The classical size-distance invariance hypothesis
Conventional "textbook" theories of "size" and distance perception do not refer to the perceived visual angle (e.g., Gregory, 1963, 1970, 1998, 2008) and some researchers even deny that it exists (Kaufman & Kaufman, 2002). This idea that one does not see the different directions in which objects lie from oneself is a basis of the so-called "size-distance invariance hypothesis" (SDIH).That old SDIH logic (geometry) is typically illustrated using a diagram that resembles Figure 2, but has the physical visual angle θ substituted for the perceived visual angle θ′. The equation for the SDIH thus is
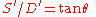
Here, S′ is typically called the "perceived size" or "apparent size"; more precisely it is the perceived linear size, measured in meters.
When rearranged as S′ = D′ tan θ, the equation expresses Emmert's law
Emmert's law
Emmert's Law bears the name of Emil Emmert , since it was first described by him in 1881. Emmert noted that an afterimage appeared to increase in size when projected to a greater distance. It is unclear whether he intended this to mean physical distance or perceived distance, but most authors...
.
However, at least since 1962, researchers have pointed out that many classic "size" and distance illusions 3 can be neither described nor explained using the SDIH, so a new hypothesis is needed (Boring 1962, Gruber, 1956, McCready, 1965, Baird, 1970, Ono 1970). For instance, consider the simple Ebbinghaus illusion.
Example: the Ebbinghaus illusion
The two central circles are the same linear size S and the same viewing distance D, so they subtend the same visual angle θ and form equal-sized retinal images. But the lower one "looks larger" than the upper one.According to the SDIH, "looks larger" can mean only that S′ is greater, and with the physical angle θ the same for both, the SDIH requires that D′ be greater for the lower one than for the upper one. However, for most observers, both circles appear unequal while also appearing at the same distance (on the same page).
This commonly found disagreement between published data and the SDIH is known as the "size-distance paradox" (Gruber, 1956, Ono, et al. 1974).
The "paradox" completely vanishes, however, when the illusion is described, instead, as basically a visual angle illusion: That is, the perceived visual angle θ′ is larger for the lower circle than for the upper circle: It is as if its retinal image were larger.
So. according to the "new" perceptual invariance hypothesis, (S′/D′ = tan θ′), with θ′ larger for the lower circle, and with D′ correctly the same for both circles, then S′ becomes larger for the lower one by the same ratio that θ′ is larger. That is, the reason the lower one looks a larger linear size on the page is because it looks a larger angular size than the upper one.
Explaining visual angle illusions remains difficult
The new hypothesis that includes θ′ along with S′ describes the Ebbinghaus Illusion and many other classic "size" illusions more completely and more logically than does the popular SDIH. What still needs to be explained, however, is why the basic visual angle illusion occurs in each example.Describing the few existing explanations for visual angle illusions is beyond the scope of this present entry. The most recent theories have been presented mostly in articles concerning the moon illusion (Baird et al., 1990, Enright, 1989a, 1989b, Hershenson, 1982, 1989b, Higashiyama, 1992, McCready 1986, 1999-2007, Plug & Ross, 1989, Reed, 1989, Roscoe, 1989, and especially in two "moon illusion" books (Hershenson, 1989; Ross & Plug, 2002) which make it quite clear that vision scientists have not yet agreed upon any particular theory of visual angle illusions.
There also is the lesser-known, but evidently the largest visual angle illusion of oculomotor micropsia (convergence micropsia
Convergence micropsia
Convergence micropsia is a type of micropsia characterized by the reduction in apparent size of objects viewed when the eyes are more converged than they need to be for the distance of the object from the eyes....
) for which a few different explanations are being considered (McCready, 1965, 2007, Ono, 1970, Komoda & Ono, 1974, Ono, et al. 1974, Enright, 1987b, 1989a, 1989b).
This is a partial list of "size and distance" illusions that begin as visual angle illusions (angular size illusions) for most observers.
- Moon illusionMoon illusionThe Moon illusion is an optical illusion in which the Moon appears larger near the horizon than it does while higher up in the sky. This optical illusion also occurs with the sun and star constellations. It has been known since ancient times, and recorded by numerous different cultures...
- Oculomotor micropsia (convergence micropsiaConvergence micropsiaConvergence micropsia is a type of micropsia characterized by the reduction in apparent size of objects viewed when the eyes are more converged than they need to be for the distance of the object from the eyes....
) - Ebbinghaus illusionEbbinghaus illusionThe Ebbinghaus illusion or Titchener circles is an optical illusion of relative size perception. In the best-known version of the illusion, two circles of identical size are placed near to each other and one is surrounded by large circles while the other is surrounded by small circles; the first...
(Titchner circles) - Hering illusionHering illusionThe Hering illusion is a one of the geometrical-optical illusions and was discovered by the German physiologist Ewald Hering in 1861 . Two straight and parallel lines look as if they were bowed outwards. The distortion is produced by the radiating pattern and was ascribed by Hering to an...
- Ponzo illusionPonzo illusionThe Ponzo illusion is a geometrical-optical illusion that was first demonstrated by the Italian psychologist Mario Ponzo in 1913. He suggested that the human mind judges an object's size based on its background. He showed this by drawing two identical lines across a pair of converging lines,...
- Müller-Lyer illusion
- Orbison illusionOrbison illusionThe Orbison illusion is an optical illusion that was first described by the psychologist William Orbison in 1939. The bounding rectangle and inner square both appear distorted in the presence of the radiating lines. The background gives us the impression there is some sort of perspective. As a...
- Jastrow illusionJastrow illusionThe Jastrow illusion is an optical illusion discovered by the American psychologist Joseph Jastrow in 1889. In this illustration, the two figures are identical, although the lower one appears to be larger. The short edge of the upper figure is compared to the long side of the lower one....
- Wundt illusionWundt illusionThe Wundt illusion is an optical illusion that was first described by the German psychologist Wilhelm Wundt in the 19th century. The two red vertical lines are both straight, but they may look as if they are bowed inwards to some observers. The distortion is induced by the crooked lines on the...
- Curvature of the apparent fronto-parallel plane (AFPP)

