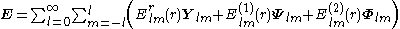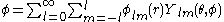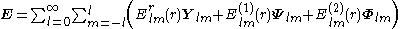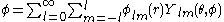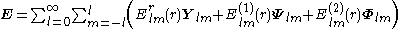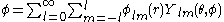Vector spherical harmonics
Encyclopedia
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics
for the use with vector field
s.
We follow that of Barrera et al.. Given a scalar spherical harmonic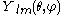 we define three VSH:
we define three VSH:
being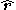 the unitary vector along the radial direction and
the unitary vector along the radial direction and 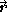 the position vector of the point with spherical coordinates
the position vector of the point with spherical coordinates  ,
,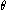 and
and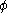 . The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
. The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
The interest of these new vector fields is to separate the radial dependence from the angular one when using spherical coordinates, so that a vector field admits a multipole expansion
The labels on the components reflect that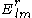 is the radial component of the vector field, while
is the radial component of the vector field, while 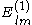 and
and 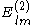 are transverse components.
are transverse components.


but also in the Hilbert space









of a scalar field
we can express its gradient in terms of the VSH as
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
for the use with vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.
Definition
Several conventions have been used to define the VSH.We follow that of Barrera et al.. Given a scalar spherical harmonic
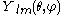 we define three VSH:
we define three VSH:being
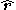 the unitary vector along the radial direction and
the unitary vector along the radial direction and 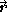 the position vector of the point with spherical coordinates
the position vector of the point with spherical coordinates  ,
,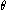 and
and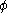 . The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
. The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.The interest of these new vector fields is to separate the radial dependence from the angular one when using spherical coordinates, so that a vector field admits a multipole expansion
Multipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
The labels on the components reflect that
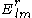 is the radial component of the vector field, while
is the radial component of the vector field, while 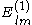 and
and 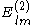 are transverse components.
are transverse components.Symmetry
Like the scalar spherical harmonics, the VSH satisfy
Orthogonality
The VSH are orthogonal in the usual three-dimensional way
but also in the Hilbert space






Vector multipole moments
The orthogonality relations allow to compute the spherical multipole moments of a vector field as


The gradient of a scalar field
Given the multipole expansionMultipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
of a scalar field
we can express its gradient in terms of the VSH as
-
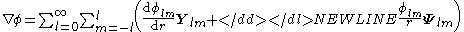
Divergence
For any multipole field we have
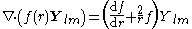
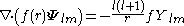
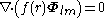
By superposition we obtain the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of any vector field
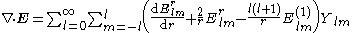
we see that the component on is always solenoidal.
is always solenoidal.
Curl
For any multipole field we have
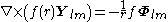
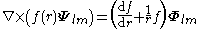
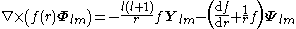
By superposition we obtain the curl of any vector field
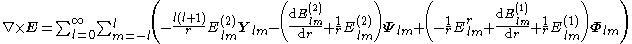
First vector spherical harmonics
The expression for negative values of m are obtained applying the symmetry relations.
Application to electrodynamics
The VSH are especially useful in the study of multipole radiation fields. For instance, a magnetic multipole is due to an oscillating current with angular frequency and complex amplitude
and complex amplitude
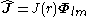
and the corresponding electric and magnetic fields can be written as
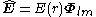
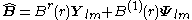
Substituting into Maxwell equations, Gauss' law is automatically satisfied
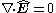
while Faraday's law decouples in
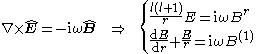
Gauss' law for the magnetic field implies
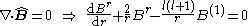
and Ampère-Maxwell's equation gives
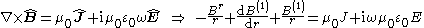
In this way, the partial differential equations have been transformed in a set of ordinary differential equations.
Application to fluid dynamics
In the calculation of the Stokes' lawStokes' lawIn 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
for the drag that a viscous fluid exerts on a small spherical particle, the velocity distribution obeys Navier-Stokes equationsNavier-Stokes equationsIn physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
neglecting inertia, i.e.
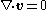
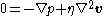
with the boundary conditions
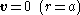
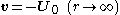
being the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
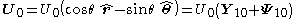
The last expression suggest an expansion on spherical harmonics for the liquid velocity and the pressure
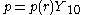
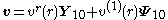
Substitution in the Navier-Stokes equations produces a set of ordinary differential equations for the coefficients.
See also
- Spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
- Spin spherical harmonicsSpin spherical harmonicsIn quantum mechanics, spin spherical harmonics are spinors that are eigenstates of the square of the angular momentum operator, and so are the natural spinorial analog of vector spherical harmonics.They are given in matrix form...
- Multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
- Electromagnetic radiationElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
- Spherical coordinates
External links
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
for the use with vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.
Definition
Several conventions have been used to define the VSH.
We follow that of Barrera et al.. Given a scalar spherical harmonic we define three VSH:
we define three VSH:
being the unitary vector along the radial direction and
the unitary vector along the radial direction and  the position vector of the point with spherical coordinates
the position vector of the point with spherical coordinates  ,
, and
and . The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
. The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
The interest of these new vector fields is to separate the radial dependence from the angular one when using spherical coordinates, so that a vector field admits a multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
The labels on the components reflect that is the radial component of the vector field, while
is the radial component of the vector field, while  and
and  are transverse components.
are transverse components.
Symmetry
Like the scalar spherical harmonics, the VSH satisfy
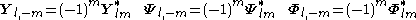
Orthogonality
The VSH are orthogonal in the usual three-dimensional way
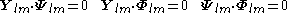
but also in the Hilbert space
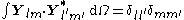
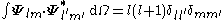
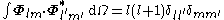
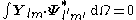
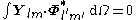
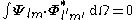
Vector multipole moments
The orthogonality relations allow to compute the spherical multipole moments of a vector field as
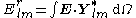
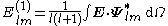
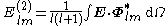
The gradient of a scalar field
Given the multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
of a scalar field
we can express its gradient in terms of the VSH as
-
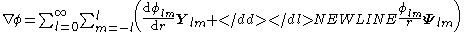
Divergence
For any multipole field we have
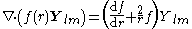
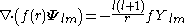
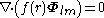
By superposition we obtain the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of any vector field
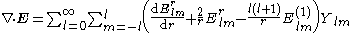
we see that the component on is always solenoidal.
is always solenoidal.
Curl
For any multipole field we have
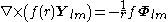
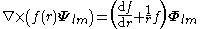
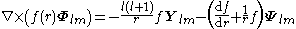
By superposition we obtain the curl of any vector field
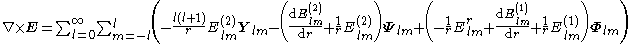
First vector spherical harmonics
The expression for negative values of m are obtained applying the symmetry relations.
Application to electrodynamics
The VSH are especially useful in the study of multipole radiation fields. For instance, a magnetic multipole is due to an oscillating current with angular frequency and complex amplitude
and complex amplitude
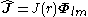
and the corresponding electric and magnetic fields can be written as
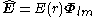
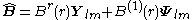
Substituting into Maxwell equations, Gauss' law is automatically satisfied
while Faraday's law decouples in
Gauss' law for the magnetic field implies
and Ampère-Maxwell's equation gives
In this way, the partial differential equations have been transformed in a set of ordinary differential equations.
Application to fluid dynamics
In the calculation of the Stokes' lawStokes' lawIn 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
for the drag that a viscous fluid exerts on a small spherical particle, the velocity distribution obeys Navier-Stokes equationsNavier-Stokes equationsIn physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
neglecting inertia, i.e.
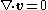
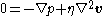
with the boundary conditions
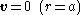
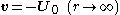
being the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
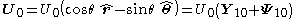
The last expression suggest an expansion on spherical harmonics for the liquid velocity and the pressure
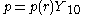
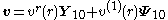
Substitution in the Navier-Stokes equations produces a set of ordinary differential equations for the coefficients.
See also
- Spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
- Spin spherical harmonicsSpin spherical harmonicsIn quantum mechanics, spin spherical harmonics are spinors that are eigenstates of the square of the angular momentum operator, and so are the natural spinorial analog of vector spherical harmonics.They are given in matrix form...
- Multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
- Electromagnetic radiationElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
- Spherical coordinates
External links
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
for the use with vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.
Definition
Several conventions have been used to define the VSH.
We follow that of Barrera et al.. Given a scalar spherical harmonic we define three VSH:
we define three VSH:
being the unitary vector along the radial direction and
the unitary vector along the radial direction and  the position vector of the point with spherical coordinates
the position vector of the point with spherical coordinates  ,
, and
and . The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
. The radial factors are included to guarantee that the dimensions of the VSH are the same as the ordinary spherical harmonics and that the VSH do not depend on the radial spherical coordinate.
The interest of these new vector fields is to separate the radial dependence from the angular one when using spherical coordinates, so that a vector field admits a multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
The labels on the components reflect that is the radial component of the vector field, while
is the radial component of the vector field, while  and
and  are transverse components.
are transverse components.
Symmetry
Like the scalar spherical harmonics, the VSH satisfy
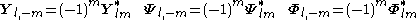
Orthogonality
The VSH are orthogonal in the usual three-dimensional way
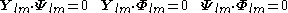
but also in the Hilbert space
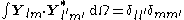
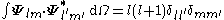
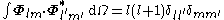
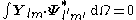
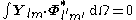
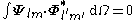
Vector multipole moments
The orthogonality relations allow to compute the spherical multipole moments of a vector field as
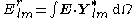
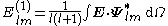
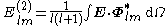
The gradient of a scalar field
Given the multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
of a scalar field
we can express its gradient in terms of the VSH as
-
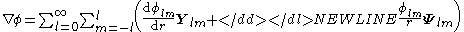
Divergence
For any multipole field we have
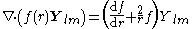
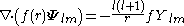
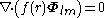
By superposition we obtain the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of any vector field
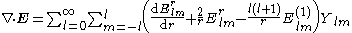
we see that the component on is always solenoidal.
is always solenoidal.
Curl
For any multipole field we have
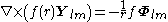
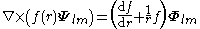
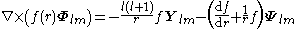
By superposition we obtain the curl of any vector field
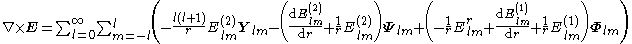
First vector spherical harmonics
The expression for negative values of m are obtained applying the symmetry relations.
Application to electrodynamics
The VSH are especially useful in the study of multipole radiation fields. For instance, a magnetic multipole is due to an oscillating current with angular frequency and complex amplitude
and complex amplitude
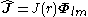
and the corresponding electric and magnetic fields can be written as
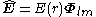
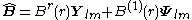
Substituting into Maxwell equations, Gauss' law is automatically satisfied
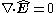
while Faraday's law decouples in
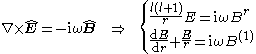
Gauss' law for the magnetic field implies
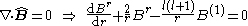
and Ampère-Maxwell's equation gives
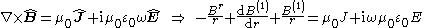
In this way, the partial differential equations have been transformed in a set of ordinary differential equations.
Application to fluid dynamics
In the calculation of the Stokes' lawStokes' lawIn 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
for the drag that a viscous fluid exerts on a small spherical particle, the velocity distribution obeys Navier-Stokes equationsNavier-Stokes equationsIn physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
neglecting inertia, i.e.
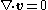
with the boundary conditions
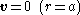
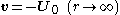
being the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
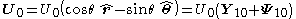
The last expression suggest an expansion on spherical harmonics for the liquid velocity and the pressure
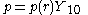
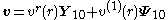
Substitution in the Navier-Stokes equations produces a set of ordinary differential equations for the coefficients.
See also
- Spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
- Spin spherical harmonicsSpin spherical harmonicsIn quantum mechanics, spin spherical harmonics are spinors that are eigenstates of the square of the angular momentum operator, and so are the natural spinorial analog of vector spherical harmonics.They are given in matrix form...
- Multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
- Electromagnetic radiationElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
- Spherical coordinates
External links
-
-
-