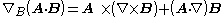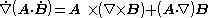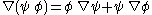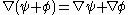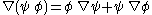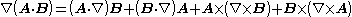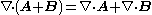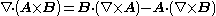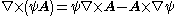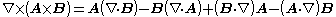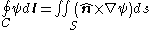Vector calculus identities
Encyclopedia
The following identities are important in vector calculus:
,
, of order n, is generally written as
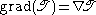
and is a tensor of order n+1. In particular, if the tensor is order 0 (i.e. a scalar),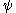
, the resulting gradient,
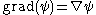
is a vector field.
, , of non-zero order n, is generally written as
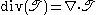
and is a contraction to a tensor of order n-1. Specifically, the divergence of a vector is a scalar. The divergence of a higher order tensor may be found by decomposing the tensor into a sum of outer products, thereby allowing the use of the identity,
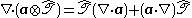
where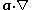
is the directional derivative
in the direction of
multiplied by its magnitude. Specifically, for the outer product of two vectors,
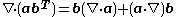
, curl is generally written as:
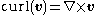
and is also a 3-dimensional vector field.
,
, the laplacian is generally written as:
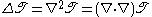
and is a tensor of the same order.
where the notation ∇B means the subscripted gradient operates on only the factor B.
A less general but similar idea is used in geometric algebra
where the so-called Hestenes overdot notation is employed. The above identity is then expressed as:
where overdots define the scope of the vector derivative. The dotted vector, in this case B, is differentiated, while the (undotted) A is held constant.
For the remainder of this article, Feynman subscript notation will be used where appropriate.
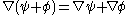
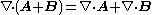
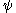and 
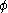follows the same form as the product rule
in single variable calculus
.
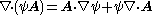
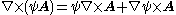
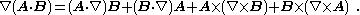
Alternatively, using Feynman subscript notation,
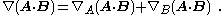
As a special case, when A = B,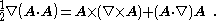
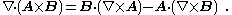
of any scalar field
is always the zero vector:
of the curl of any vector field
A is always zero:
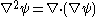
Note that the result is a scalar quantity.
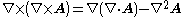
Here, ∇2 is the vector Laplacian
operating on the vector field A.
Gradient
Gradient of a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
,
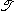, of order n, is generally written as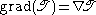and is a tensor of order n+1. In particular, if the tensor is order 0 (i.e. a scalar),
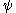, the resulting gradient,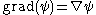is a vector field.
Divergence
Divergence of a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, , of non-zero order n, is generally written as
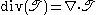
and is a contraction to a tensor of order n-1. Specifically, the divergence of a vector is a scalar. The divergence of a higher order tensor may be found by decomposing the tensor into a sum of outer products, thereby allowing the use of the identity,
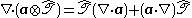
where
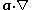is the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
in the direction of
multiplied by its magnitude. Specifically, for the outer product of two vectors,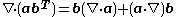Curl
For a 3-dimensional vector field, curl is generally written as: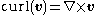and is also a 3-dimensional vector field.
Laplacian
For a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
,
, the laplacian is generally written as: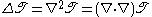and is a tensor of the same order.
Special notations
In Feynman subscript notation,
where the notation ∇B means the subscripted gradient operates on only the factor B.
A less general but similar idea is used in geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
where the so-called Hestenes overdot notation is employed. The above identity is then expressed as:
where overdots define the scope of the vector derivative. The dotted vector, in this case B, is differentiated, while the (undotted) A is held constant.
For the remainder of this article, Feynman subscript notation will be used where appropriate.
Distributive properties
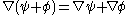
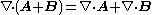
Product rule for the gradient
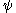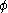The gradient of the product of two scalar fields and follows the same form as the product ruleProduct rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
in single variable calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
Product of a scalar and a vector
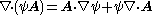
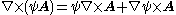
Vector dot product
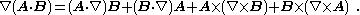
Alternatively, using Feynman subscript notation,
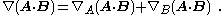
As a special case, when A = B,
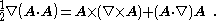
Vector cross product
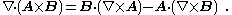
Curl of the gradient
The curl of the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of any scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
is always the zero vector:Divergence of the curl
The divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the curl of any vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
A is always zero:
Divergence of the gradient
The Laplacian of a scalar field is defined as the divergence of the gradient: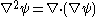Note that the result is a scalar quantity.
Curl of the curl
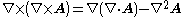
Here, ∇2 is the vector Laplacian
Vector Laplacian
In mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
operating on the vector field A.
Addition and multiplication
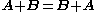
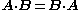
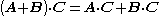
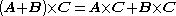
(scalar triple product)
(vector triple product)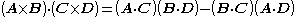
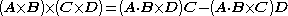
Differentiation
Gradient
Divergence
Curl
Second derivatives
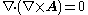
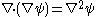(scalar LaplacianLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
)
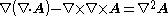(vector LaplacianVector LaplacianIn mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
)
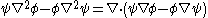
Integration
(Divergence theoremDivergence theoremIn vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
)
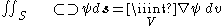
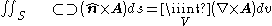
(Green's first identity)
(Green's second identity)
(Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
)
See also
- exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
- Vector calculus
- Del in cylindrical and spherical coordinatesDel in cylindrical and spherical coordinatesThis is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
- Comparison of vector algebra and geometric algebraComparison of vector algebra and geometric algebraVector algebra and geometric algebra are alternative approaches to providing additional algebraic structures on vector spaces, with geometric interpretations, particularly vector fields in multivariable calculus and applications in mathematical physics....